Motif Search (Motif Search)
Jump to navigation
Jump to search
Description
Motif search is the problem of identifying motifs, recurring or conserved patterns, in the strings (typically biological sequence data sets).
Parameters
$n$: size of set of input strings
$m$: size of input strings
$k$: length of substrings
$\sigma$: function $V(k, m)$ defined as the number of $k$-mers that are at most $m$ Hamming distance from the motif space
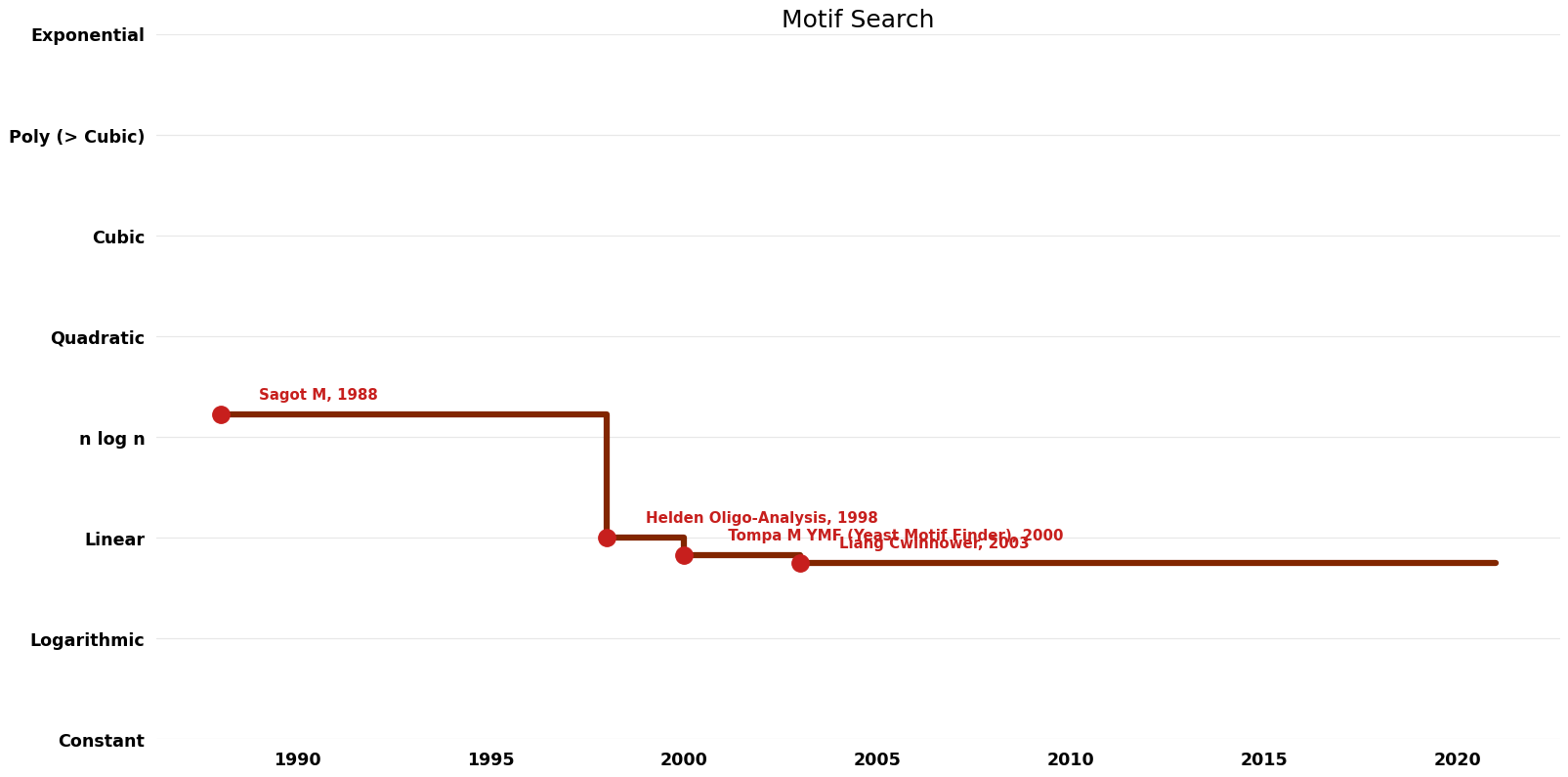
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Lawrence, Reilly | 1990 | $O(nm)$ | $O(nm)$ | Deterministic | Time & Space | |
| Lawrence Gibbs Sampling | 1993 | $O(nm)$ | $O(n + m)$ | Deterministic | Time | |
| MotifSampler | 2001 | $O(nm)$ | $O(n + m)$ | Deterministic | Time | |
| Speller | 1998 | $O(mn^{2} \sigma)$ | $O(mn^{2}/w)$ | Exact | Deterministic | Time & Space |
| Mitra | 2002 | $O(k nm \sigma)$ | $O(mnk)$ | Exact | Deterministic | Time & Space |
| Census | 2003 | $O(k nm \sigma)$ | $O(mnk)$ | Exact | Deterministic | Time & Space |
| Risotto | 2006 | $O(mn^{2} \sigma)$ | $O(mn^{2})$ | Exact | Deterministic | Time & Space |
| PMS | 2007 | $O(nm^{2} \sigma)$ | $O(m^{2} n)$ | Exact | Deterministic | Time & Space |
| Roth AlignACE | 1998 | $O(nm)$ | $O(n + m)$ | Deterministic | Time | |
| Helden Oligo-Analysis | 1998 | $O(mn)$ | $O(m)$ | Exact | Deterministic | Time |
| van Helden J; Rios AF; Collado-Vides J | 2000 | $O(mn)$ | $O(m)$ | Exact | Deterministic | Time |
| Tompa M | 1999 | $O(mn)$ | $O(m^{2})$ | Exact | Deterministic | Time |
| Sinha S; Tompa M YMF (Yeast Motif Finder) | 2000 | $O(n^{0.{6}6} m)$ | $O(m)$ | Exact | Deterministic | Time |
| Bailey TL; Elkan C MEME | 1995 | $O(n^{2}m^{2})$ | $O(mn)$ | Exact | Deterministic | Time |
| Sagot M | 1988 | $O(n \log(n)$ m^{1.{4}5}) | $O(mn^{2}/w)$ | Exact | Deterministic | Time & Space |
| Liang Cwinnower | 2003 | $O(nm^{0.5})$ | $O(m^{2})$ | Exact | Deterministic | Time |
| Kingsford | 2006 | $O(mn)$ | $O(m^{2}n^{2})$ | Exact | Deterministic | Time |