Secret-sharing algorithms

Problem Description

Secret Sharing refers to cryptographic methods for taking a secret, breaking it up into multiple shares, and distributing the shares among multiple parties, so that only when the parties bring together their respective shares can the secret be reconstructed. More specifically, the holder of a secret, sometimes referred to as the dealer, creates n shares of a secret and defines a threshold t for the number of shares that are required to reconstruct the secret. The dealer then proceeds to distribute the shares so they are controlled by different parties.

In secure secret sharing schemes, an attacker that gains access to fewer shares of the secret than defined by the threshold gains no information about the secret.

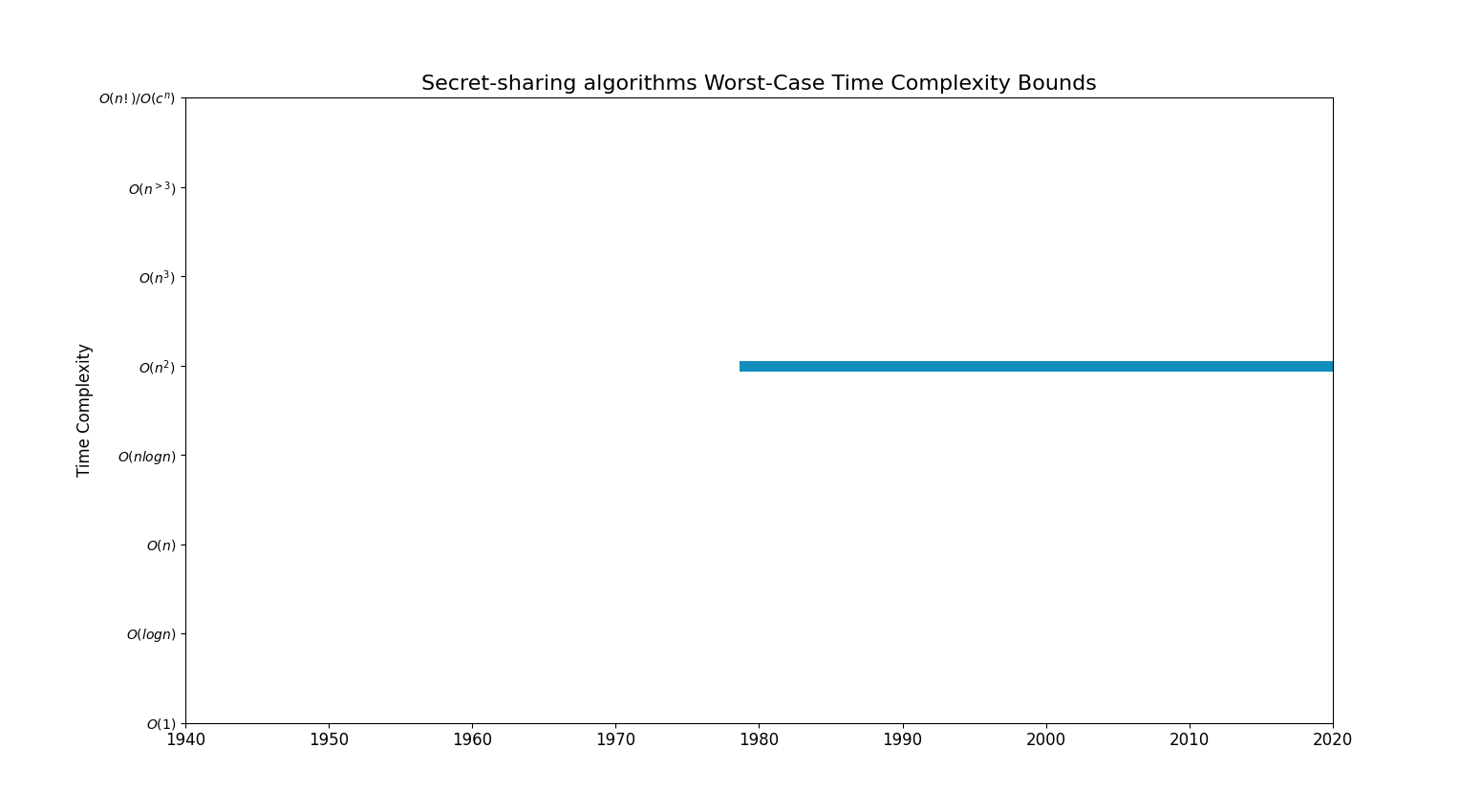
Bounds Chart

Step Chart

Improvement Table

Complexity Classes	Algorithm Paper Links	Lower Bounds Paper Links
Exp/Factorial
Polynomial > 3
Cubic
Quadratic
nlogn
Linear	[ Shamir's scheme (1979)] [ Blakley's scheme (1979)]
logn