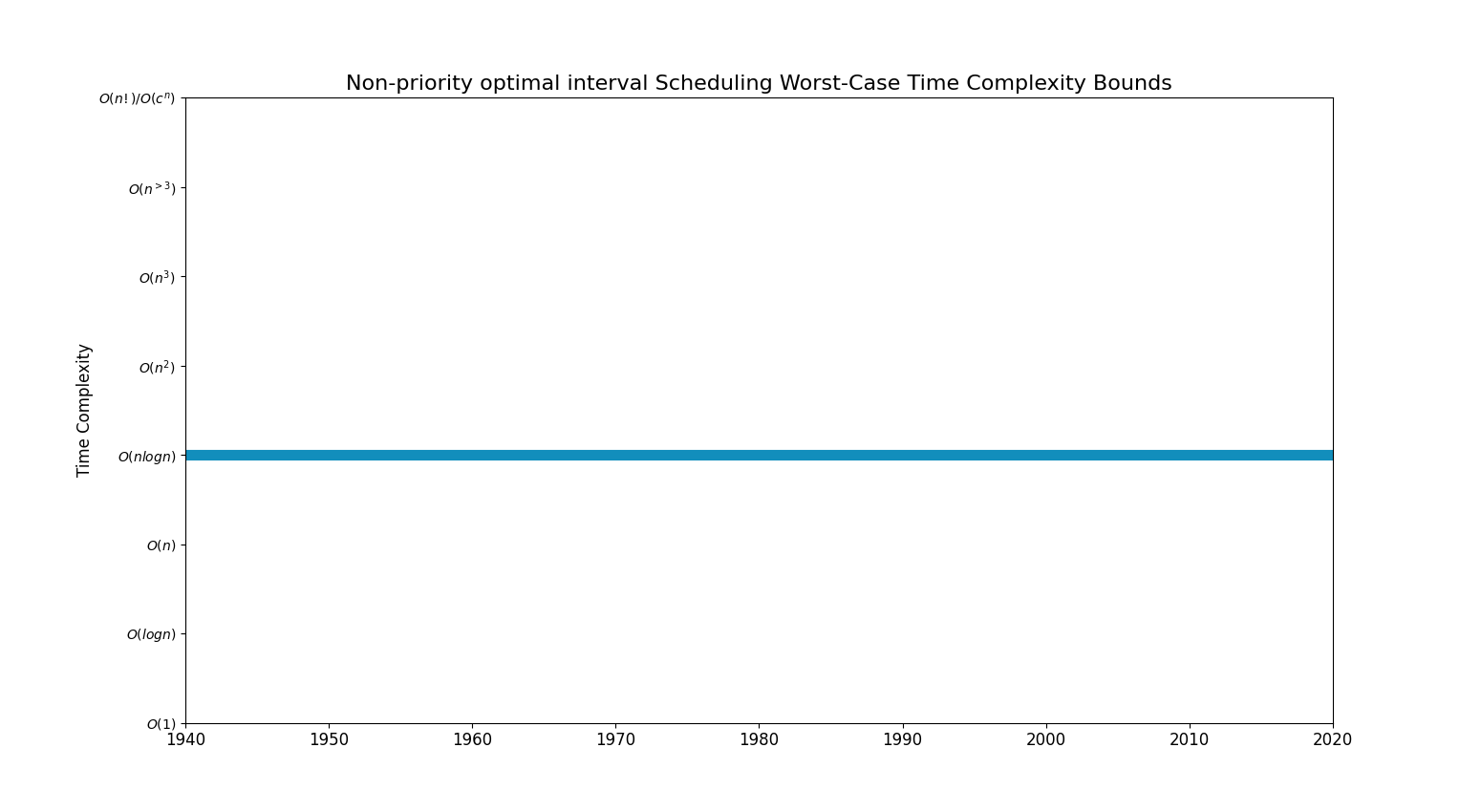
Non-priority optimal interval Scheduling
Problem Description
Interval scheduling is a class of problems in computer science, particularly in the area of algorithm design. The problems consider a set of tasks. Each task is represented by an interval describing the time in which it needs to be executed. For instance, task A might run from 2:00 to 5:00, task B might run from 4:00 to 10:00 and task C might run from 9:00 to 11:00. A subset of intervals is compatible if no two intervals overlap. For example, the subset {A,C} is compatible, as is the subset {B}; but neither {A,B} nor {B,C} are compatible subsets, because the corresponding intervals within each subset overlap.
Bounds Chart
Step Chart
Improvement Table
| Complexity Classes | Algorithm Paper Links | Lower Bounds Paper Links |
|---|---|---|
| Exp/Factorial | ||
| Polynomial > 3 | ||
| Cubic | ||
| Quadratic | ||
| nlogn | [ Fixed priority shortest job first (1940)] | |
| Linear | [ Priority scheduling (1940)]
[ Shortest remaining time first (1940)] [ First come, first served (1940)] [ Round-robin scheduling (1940)] [ Multilevel queue scheduling (1940)] [ Work-conserving schedulers (1940)] |
|
| logn |