Money Change
Jump to navigation
Jump to search
Problem Description
Given a value N, if we want to make change for N cents, and we have an infinite supply of each of S = { S1, S2, .. , Sm} valued coins, how many ways can we make the change? The order of coins doesn’t matter.
For example, for N = 4 and S = {1,2,3}, there are four solutions: {1,1,1,1},{1,1,2},{2,2},{1,3}. So output should be 4. For N = 10 and S = {2, 5, 3, 6}, there are five solutions: {2,2,2,2,2}, {2,2,3,3}, {2,2,6}, {2,3,5} and {5,5}. So the output should be 5.
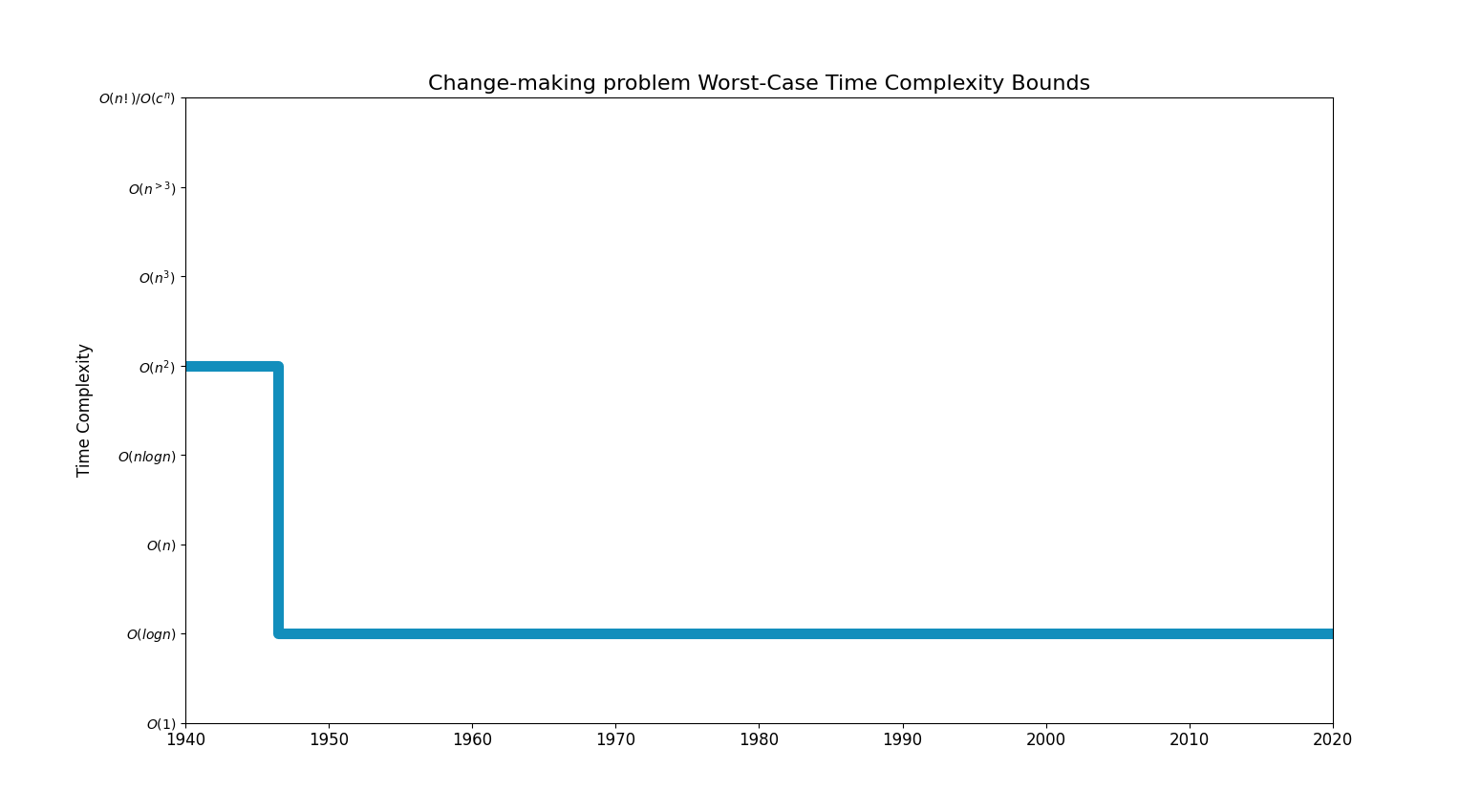
Bounds Chart
Step Chart
Improvement Table
| Complexity Classes | Algorithm Paper Links | Lower Bounds Paper Links |
|---|---|---|
| Exp/Factorial | [Brute force (1940)] | |
| Polynomial > 3 | [Dynamic Programming (1953)] | |
| Cubic | ||
| Quadratic | ||
| nlogn | ||
| Linear | ||
| logn |