Minimum value in each row of an implicitly-defined totally monotone matrix (Minimum value in each row of an implicitly-defined totally monotone matrix)
Jump to navigation
Jump to search
Description
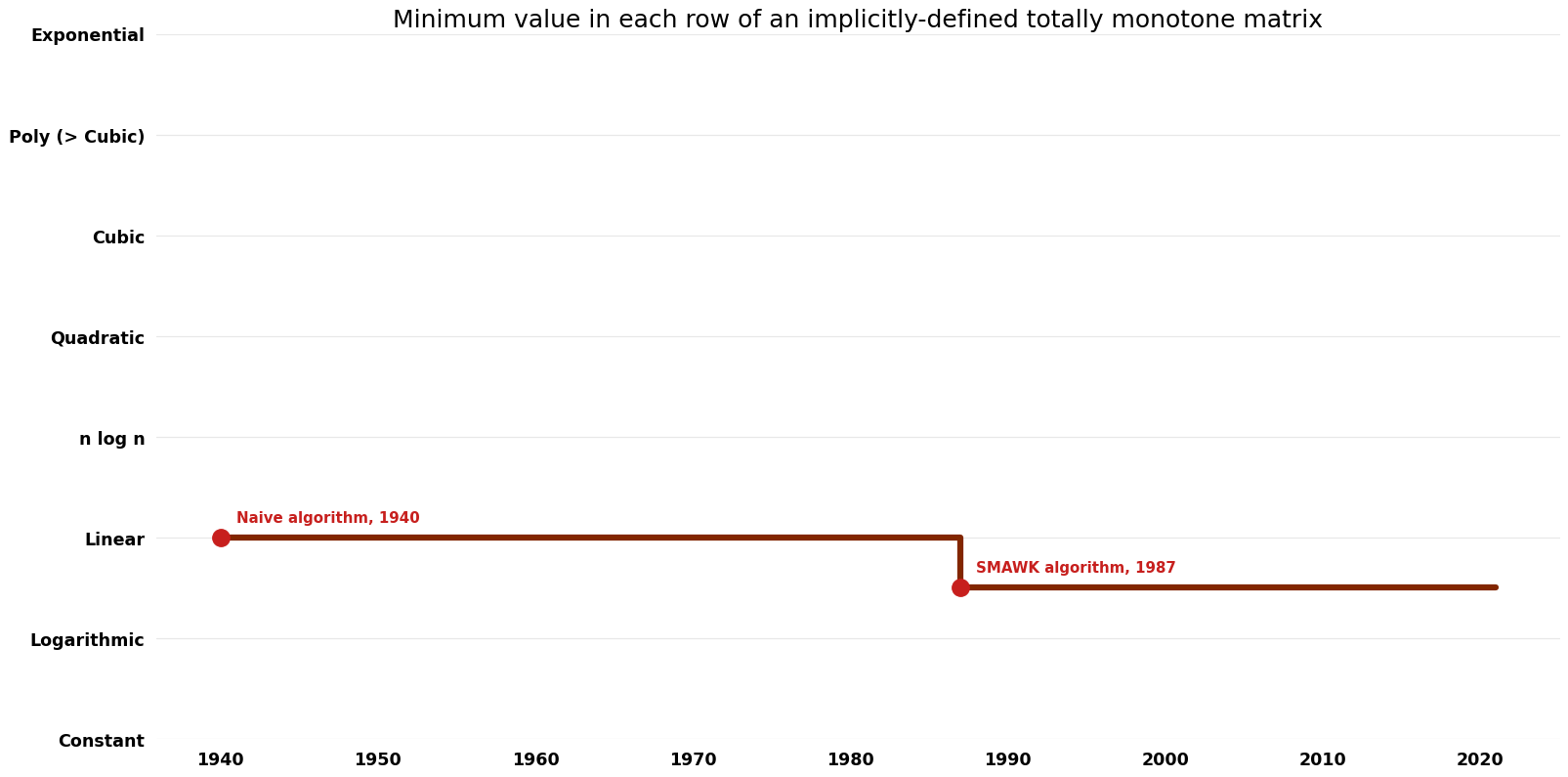
Given a totally monotone matrix $A$ whose entries $A(i, j)$ are implicitly defined by some function $f(i, j)$ (assume $f$ takes constant time to evaluate for all relevant $(i, j)$), determine the minimum value in each row.
Parameters
$m,n$: dimensions of matrix; assume $m≥n$
possibly uses a function $f$ to define entries; assume evaluation of $f$ takes time $O(1)$
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Naive algorithm | 1940 | $O(mn)$ | $O({1})$ | Exact | Deterministic | |
| SMAWK algorithm | 1987 | $O(n({1}+\log(n/m)$)) | $O(n)$? | Exact | Deterministic | Time |
| Divide and Conquer | 1987 | $O(m*log(n)$) | $O(log(n)$) auxiliary? | Exact | Deterministic | Time |
Time Complexity Graph
