Maximum cardinality matching
Problem Description
A graph is bipartite if it has two kinds of nodes and the edges are only allowed between nodes of different kind. We write G=(A,B,E) where A and B are the two sets of nodes and E are the edges of G.
A matching in a bipartite graph assigns nodes of A to nodes of B. Matchings in bipartite graphs can be computed more efficiently than matchings in general (=non-bipartite) graphs.
Interesting Fact: In a bipartite graph the maximum cardinality of a matching and the minimum cardinality of a node cover are equal.
Intuition Bipartite Matching: Suppose we have a set of workers and a set of machines. These are the two kinds of nodes in our bipartite graph. We know which worker can handle which machines. This defines the edges of our bipartite graph. Our task in the maximum cardinality matching problem is assigning workers to machines in such a way that as many machines as possible are operated by a worker that can handle it. One worker can be assigned to at most one machine and we can assign at most one worker to one machine.
Bounds Chart
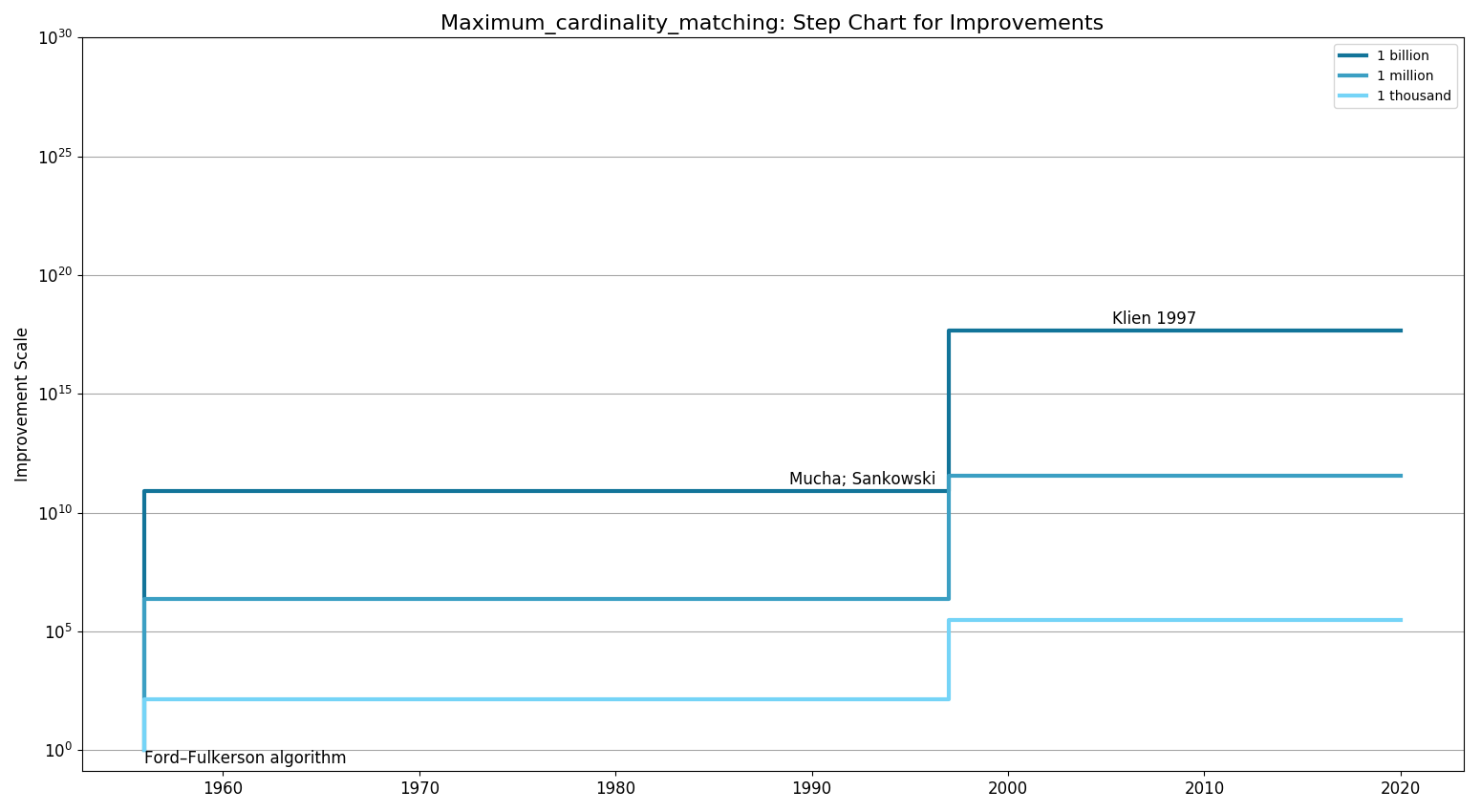
Step Chart
Improvement Table
| Complexity Classes | Algorithm Paper Links | Lower Bounds Paper Links |
|---|---|---|
| Exp/Factorial | ||
| Polynomial > 3 | ||
| Cubic | ||
| Quadratic | Ford–Fulkerson algorithm (1956)
Hopcroft–Karp algorithm (1973) [ Madry's algorithm (2009)] Chandran and Hochbaum; 2011 (2011) Gabow; Tarjan 1991 (1991) Mucha 2004 (2004) [ Klien 1997 (1997)] |
|
| nlogn | ||
| Linear | ||
| logn |