Matrix chain multiplication
Problem Description
Matrix chain multiplication (or Matrix Chain Ordering Problem, MCOP) is an optimization problem that to find the most efficient way to multiply a given sequence of matrices. The problem is not actually to perform the multiplications but merely to decide the sequence of the matrix multiplications involved. The matrix multiplication is associative as no matter how the product is parenthesized, the result obtained will remain the same.
For example, for four matrices A, B, C, and D, we would have: ((AB)C)D = ((A(BC))D) = (AB)(CD) = A((BC)D) = A(B(CD))
However, the order in which the product is parenthesized affects the number of simple arithmetic operations
needed to compute the product or the efficiency. For example, if A is a 10 x 30 matrix, B is a 30 x 5
matrix, and C is a 5 x 60 matrix, then computing (AB)C needs (10x30x5) + (10x5x60) 1500 +
3000 = 4500 operations while computing ACBC) needs (30x5x60) + (10x30x60) = 9000 + 18000
= 27000 operations. Clearly, the first method is more efficient.
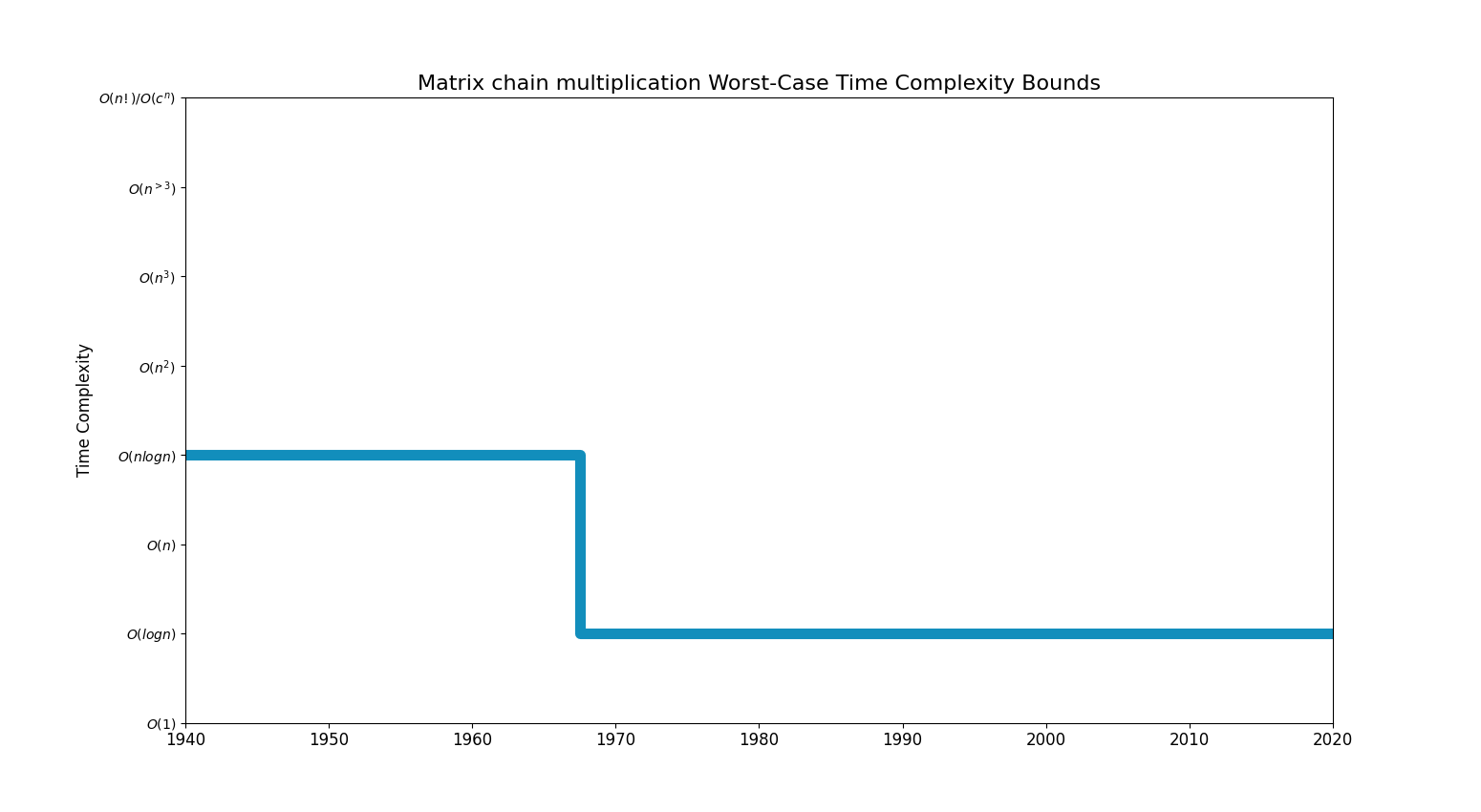
Bounds Chart
Step Chart
Improvement Table
| Complexity Classes | Algorithm Paper Links | Lower Bounds Paper Links |
|---|---|---|
| Exp/Factorial | brute force (1940) | |
| Polynomial > 3 | ||
| Cubic | dynamic programming algorithm; S. S. GODBOLE (1953) | |
| Quadratic | Heejo Lee; Jong Kim; Sungje Hong; and Sunggu Lee (1997) | |
| nlogn | T. C. Hut ; M. T. Shing (1982) | |
| Linear | Chandra 1975 (1975) | |
| Chin 1978 (1978) | ||
| logn | Prakesh Ramanan (1996) | |
| Czumaj 1992 (1992) | ||
| Czumaj 1996 (1996) |