Graph Isomorphism, General Graphs (Graph Isomorphism Problem)
Jump to navigation
Jump to search
Description
Given two graphs, determine whether they are isomorphic to one another.
Related Problems
Subproblem: Graph Isomorphism, Bounded Number of Vertices of Each Color, Graph Isomorphism, Trivalent Graphs, Graph Isomorphism, Bounded Vertex Valences, Largest Common Subtree
Related: Graph Isomorphism, Trivalent Graphs, Graph Isomorphism, Bounded Vertex Valences, Largest Common Subtree, Subtree Isomorphism
Parameters
$n$: number of vertices in the larger graph
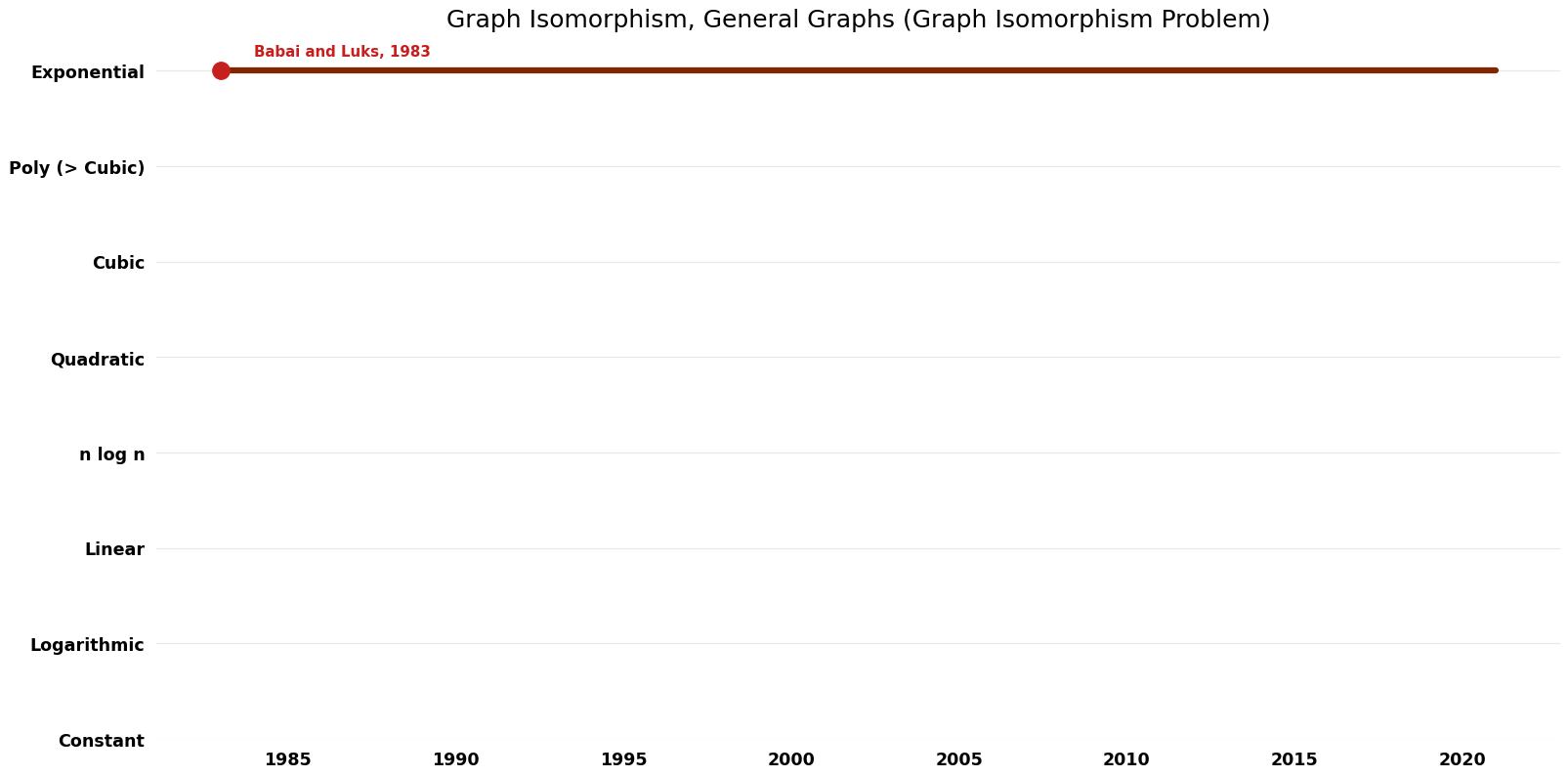
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Babai and Luks | 1983 | \exp(n^{\frac{1}{2} + o({1})}) | Exact | Deterministic | Time | |
| McKay | 1981 | $O((m1 + m2)n^{3} + m2 n^{2} L)$ | ${2}mn+{10}n+m+(m+{4})K+{2}mL$ | Exact | Deterministic | Time |
| Schmidt & Druffel | 1976 | $O(n*n!)$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Babai | 2017 | {2}^{$O(\log n)$^3} | Exact | Deterministic | Time |
Time Complexity Graph
