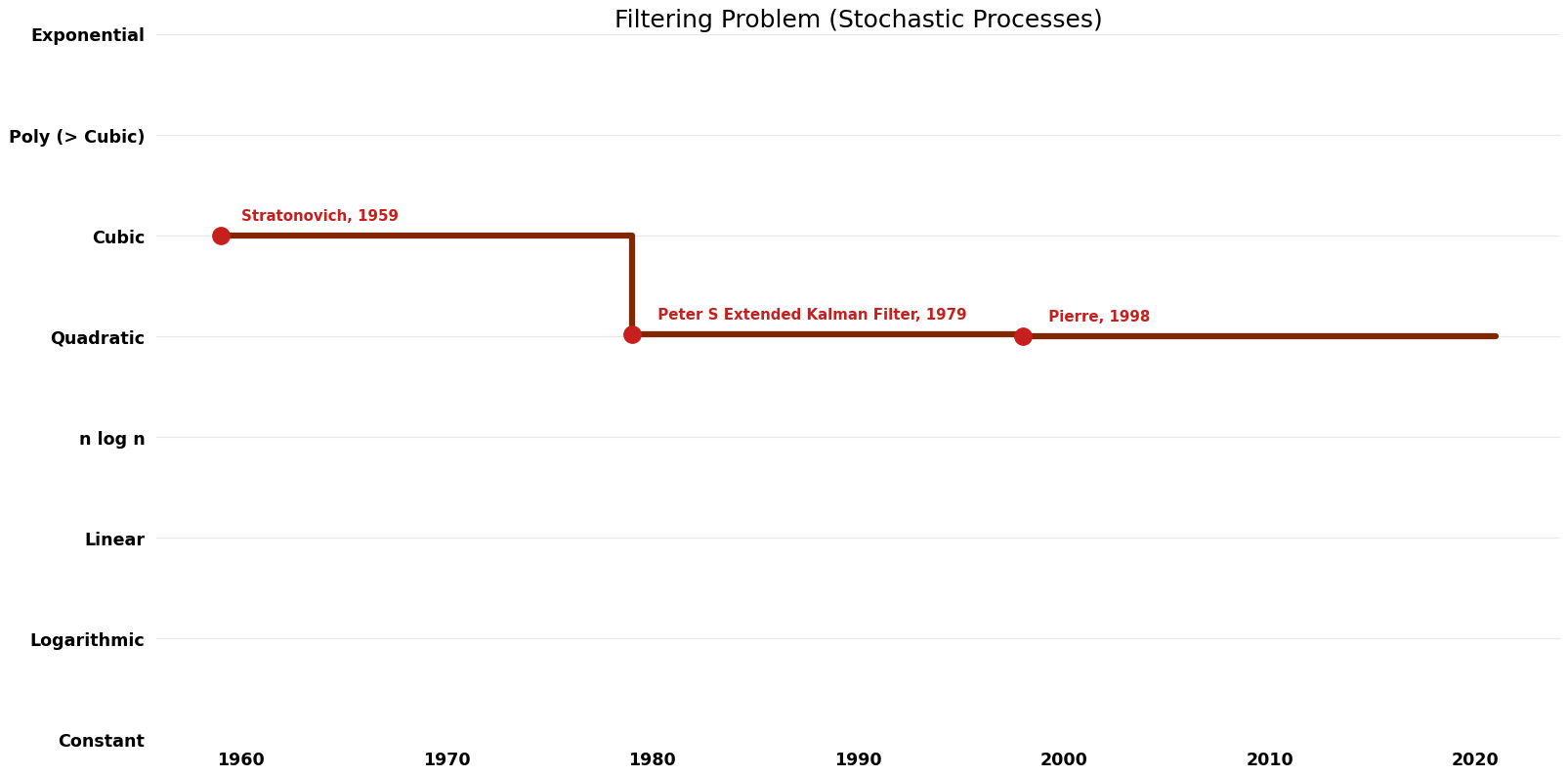
Filtering Problem (Stochastic Processes) (Filtering Problem (Stochastic Processes))
Jump to navigation
Jump to search
Description
The filtering problem is to obtain the best linear estimate $\hat{z}_t$ of $z_t$ based on the past observations ($y_s | s\leq t)$. Abstractly, the solution to the problem of filtering corresponds to explicitly computing
$\hat{z}_t = P_t^y(z_t)$
where $P_t^y$ is the projection operator onto the Hilbert space $H_t^y$.
Parameters
$n$: number of dimensions in state space
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Kalman Filter | 1960 | $O(n^{3})$ | $O(n^{2})$? | Exact | Deterministic | |
| Particle filter Del Moral | 1996 | $O(n^{3})$ | $O(nN)$? | Exact | Deterministic | |
| Stratonovich | 1959 | $O(n^{3})$ | Exact | Deterministic | ||
| Stratonovich | 1960 | $O(n^{3})$ | Exact | Deterministic | ||
| Kushner non-linear filter | 1967 | $O(n^{3})$ | $O(n^{2})$?? | Exact | Deterministic | Time |
| Zakai | 1969 | $O(n^{3})$ | Exact | Deterministic | Time | |
| Maybeck; Peter S Extended Kalman Filter | 1979 | $O(n^{2} \log^{2} n)$ | $O(n^{2})$? | Exact | Deterministic | |
| Damiano Brigo; Bernard Hanzon and François LeGland | 1998 | $O(n^{2.{4}5} \log n)$ | Exact | Deterministic | Time | |
| Del Moral; Pierre | 1998 | $O(n^{2})$ | Exact | Deterministic | Time | |
| Ocone | 1999 | $O(n^{2})$ | Exact | Deterministic | Time |