APSP on Dense Directed Graphs with Arbitrary Weights (All-Pairs Shortest Paths (APSP))
Jump to navigation
Jump to search
Description
In this case, the graph $G=(V,E)$ that we consider is dense ($m = O(n^2)$), is directed, and has arbitrary weights.
Related Problems
Generalizations: APSP
Related: APSP on Dense Undirected Graphs with Arbitrary Weights, APSP on Geometrically Weighted Graphs, APSP on Dense Undirected Graphs with Positive Integer Weights, APSP on Sparse Directed Graphs with Arbitrary Weights, APSP on Sparse Undirected Graphs with Positive Integer Weights, APSP on Sparse Undirected Graphs with Arbitrary Weights, APSP on Dense Directed Unweighted Graphs, APSP on Dense Undirected Unweighted Graphs, APSP on Sparse Directed Unweighted Graphs, APSP on Sparse Undirected Unweighted Graphs, (5/3)-approximate ap-shortest paths
Parameters
$n$: number of vertices
$m$: number of edges
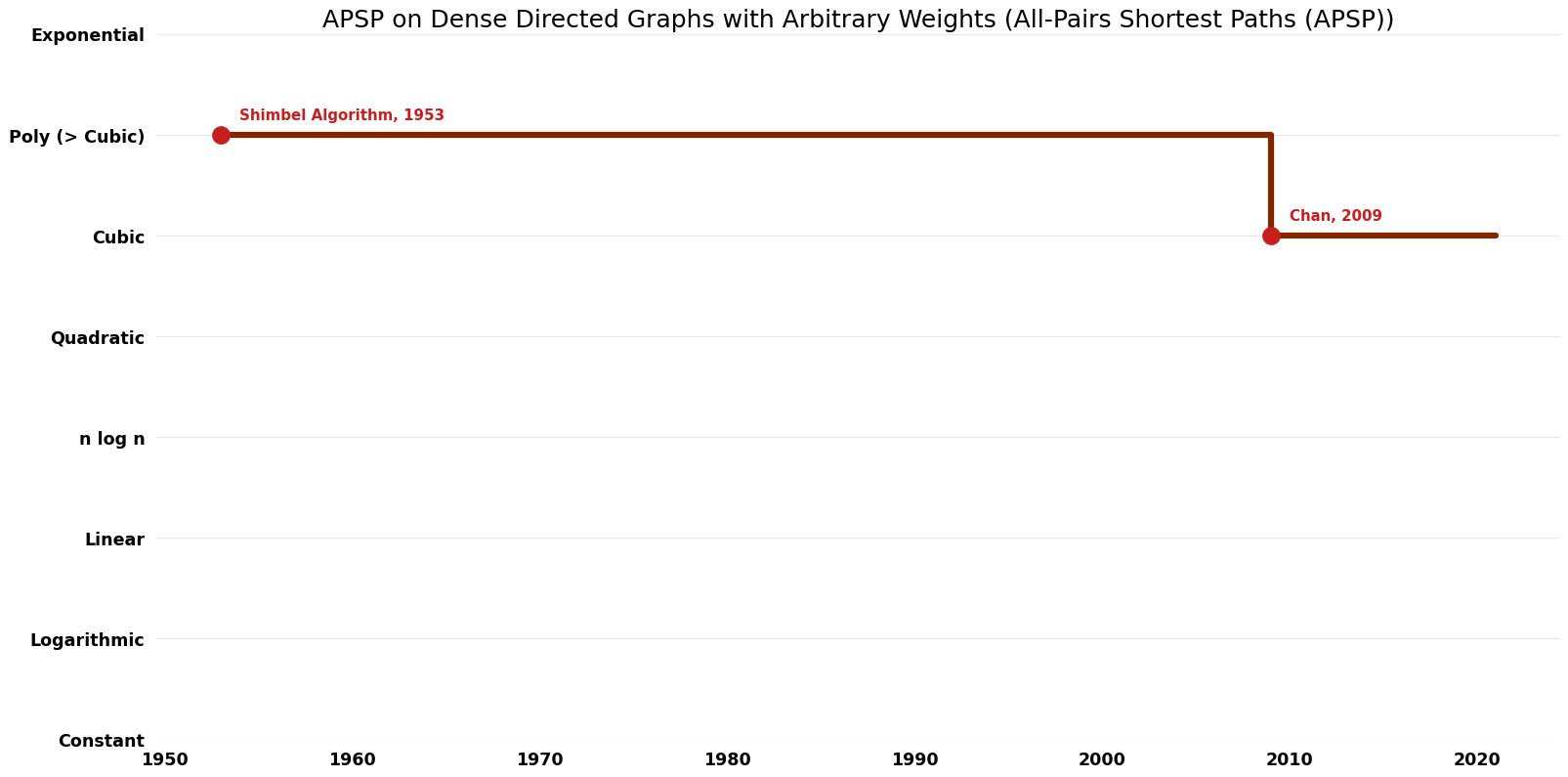
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Shimbel Algorithm | 1953 | $O(n^{4})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Williams | 2014 | $O(n^{3} /{2}^{(\log n)^{0.5}})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Chan | 2009 | $O(n^{3} \log^{3} \log n / \log^{2} n)$ | $O(n^{2})$ | Exact | Deterministic | Time |