Stable Roommates Problem (Stable Matching Problem)
Revision as of 10:23, 15 February 2023 by Admin (talk | contribs) (Created page with "{{DISPLAYTITLE:Stable Roommates Problem (Stable Matching Problem)}} == Description == Given $2n$ participants, each of participant ranks the others in strict order of preference. A matching is a set of $n$ disjoint pairs of participants. A matching $M$ in an instance of SRP is stable if there are no two participants $x$ and $y$, each of whom prefers the other to their partner in $M$. Such a pair is said to block $M$, or to be a blocking pair with respect to $M$. == Re...")
Description
Given $2n$ participants, each of participant ranks the others in strict order of preference. A matching is a set of $n$ disjoint pairs of participants. A matching $M$ in an instance of SRP is stable if there are no two participants $x$ and $y$, each of whom prefers the other to their partner in $M$. Such a pair is said to block $M$, or to be a blocking pair with respect to $M$.
Related Problems
Subproblem: Stable Marriage Problem
Related: Almost Stable Marriage Problem, Boolean d-Attribute Stable Matching, Stable Matching Verification, Stable Pair Checking
Parameters
n: number of pairs of roommates
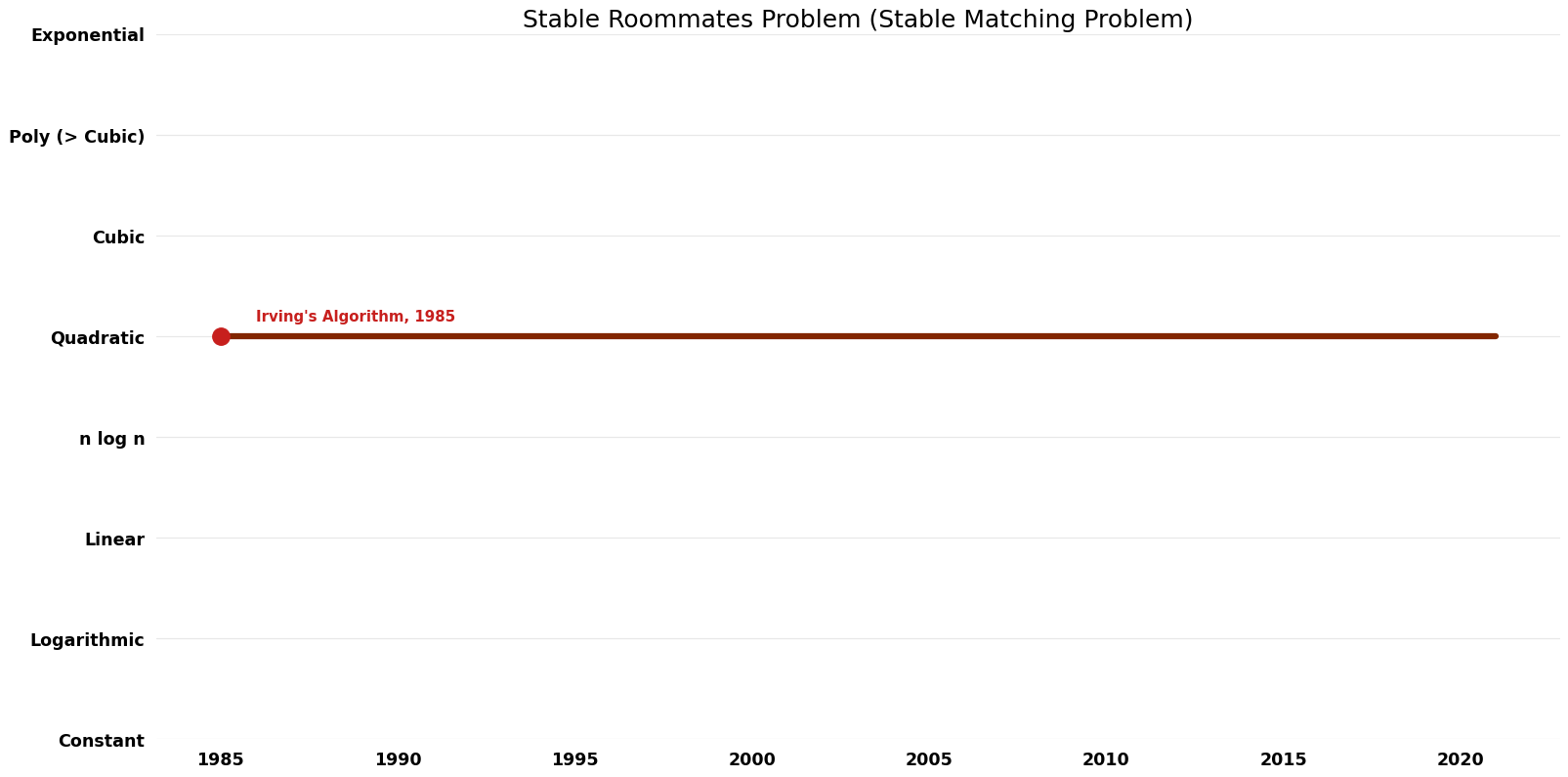
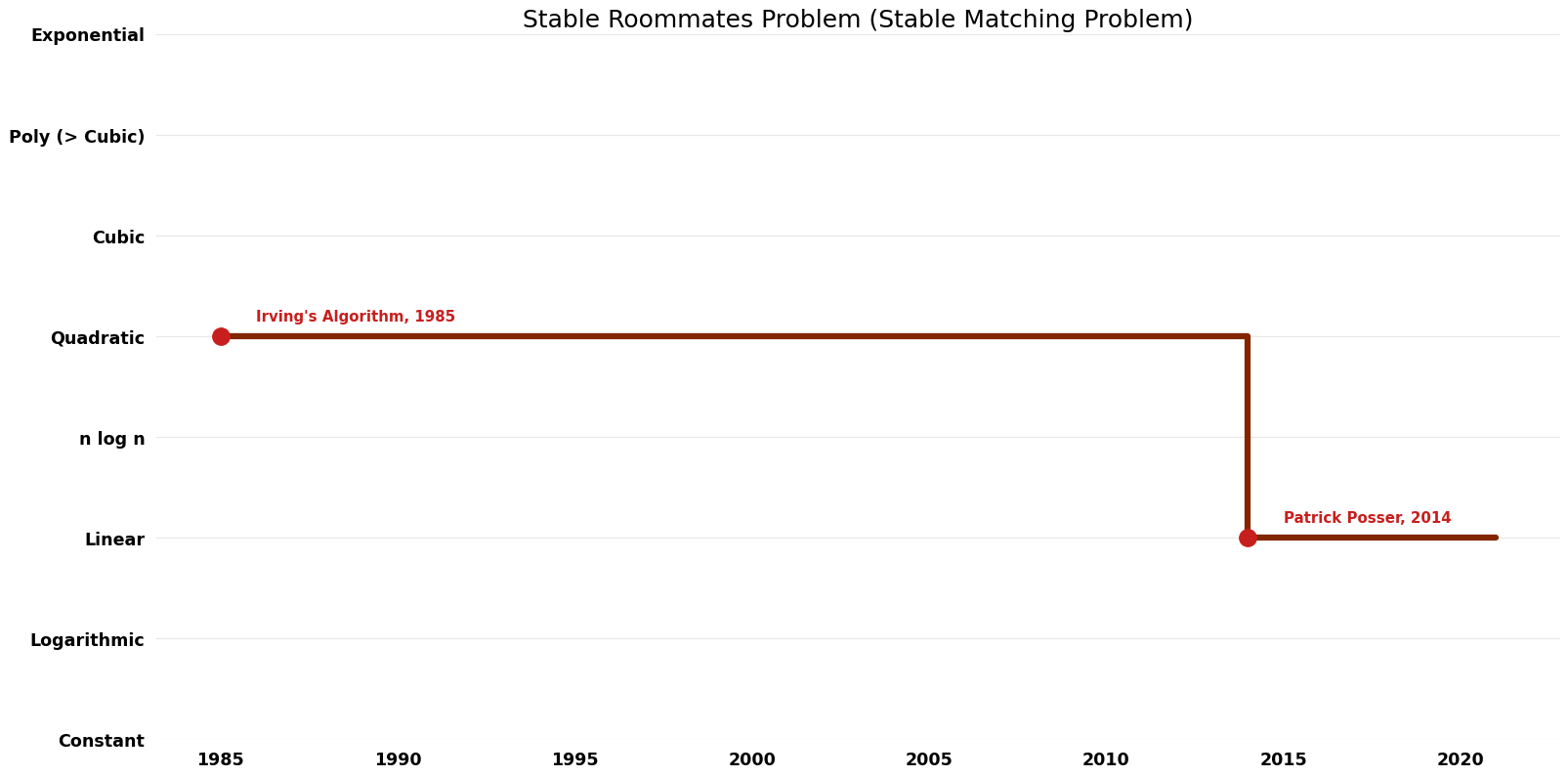
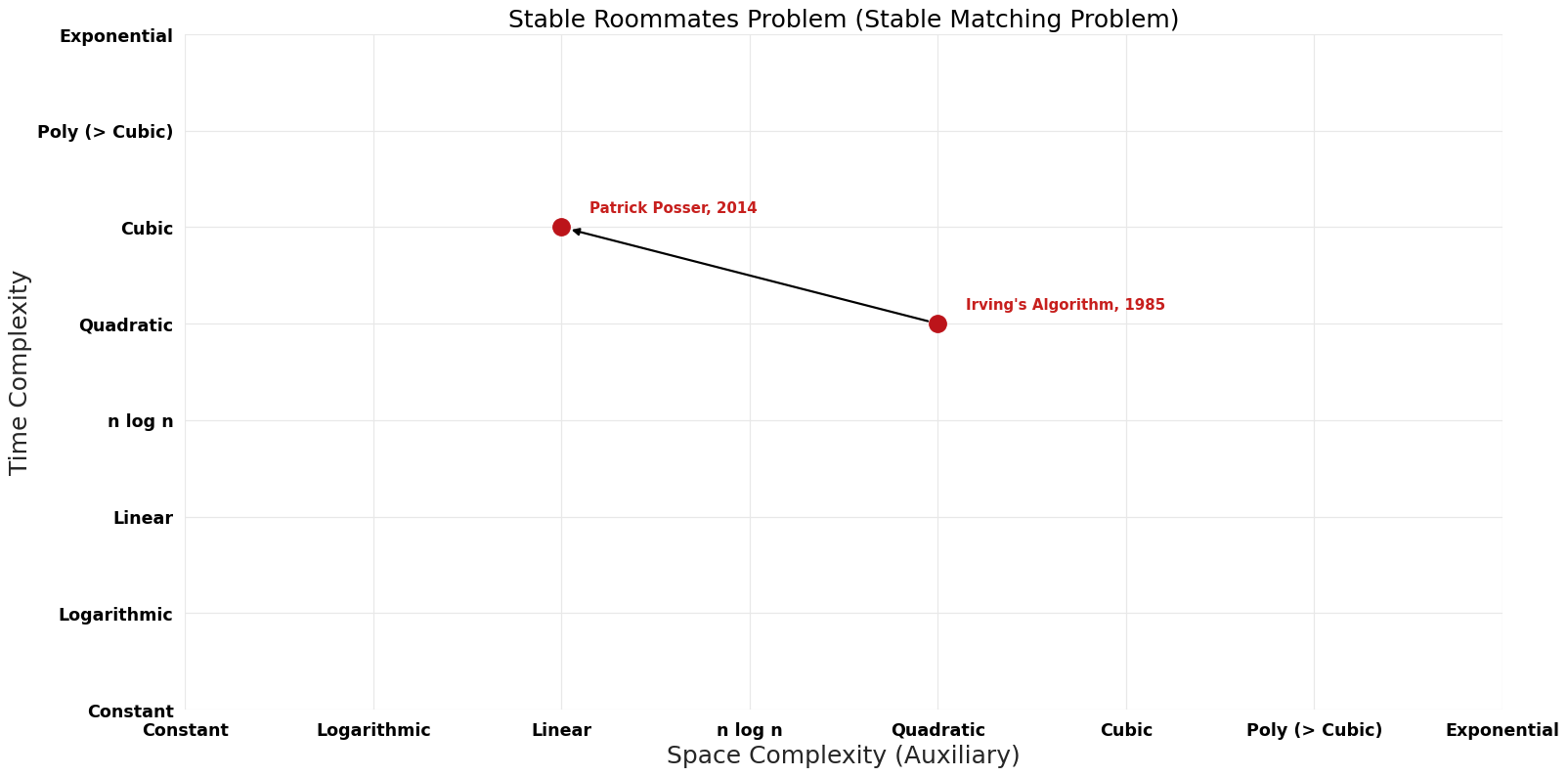
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Irving's Algorithm | 1985 | $O(n^{2})$ | $O(n^{2})$? | Exact | Deterministic | Time |
| Patrick Posser | 2014 | $O(n^{3})$ | $O(n)$ | Exact | Deterministic | Time & Space |
Time Complexity graph
Space Complexity graph
Pareto Decades graph
