Stable Marriage Problem: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 14: | Line 14: | ||
== Parameters == | == Parameters == | ||
n: number of men and number of women | $n$: number of men and number of women | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 43: | Line 43: | ||
[[File:Stable Matching Problem - Stable Marriage Problem - Time.png|1000px]] | [[File:Stable Matching Problem - Stable Marriage Problem - Time.png|1000px]] | ||
== References/Citation == | == References/Citation == | ||
http://www.dcs.gla.ac.uk/~davidm/pubs/7981.pdf | http://www.dcs.gla.ac.uk/~davidm/pubs/7981.pdf | ||
Latest revision as of 10:10, 28 April 2023
Description
Given $n$ men and $n$ women, where each person has ranked all members of the opposite sex in order of preference, marry the men and women together such that there are no two people of opposite sex who would both rather have each other than their current partners. When there are no such pairs of people, the set of marriages is deemed stable.
Related Problems
Generalizations: Stable Roommates Problem
Subproblem: Almost Stable Marriage Problem, Boolean d-Attribute Stable Matching, Stable Matching Verification, Stable Pair Checking
Related: Boolean d-Attribute Stable Matching, Stable Matching Verification, Stable Pair Checking
Parameters
$n$: number of men and number of women
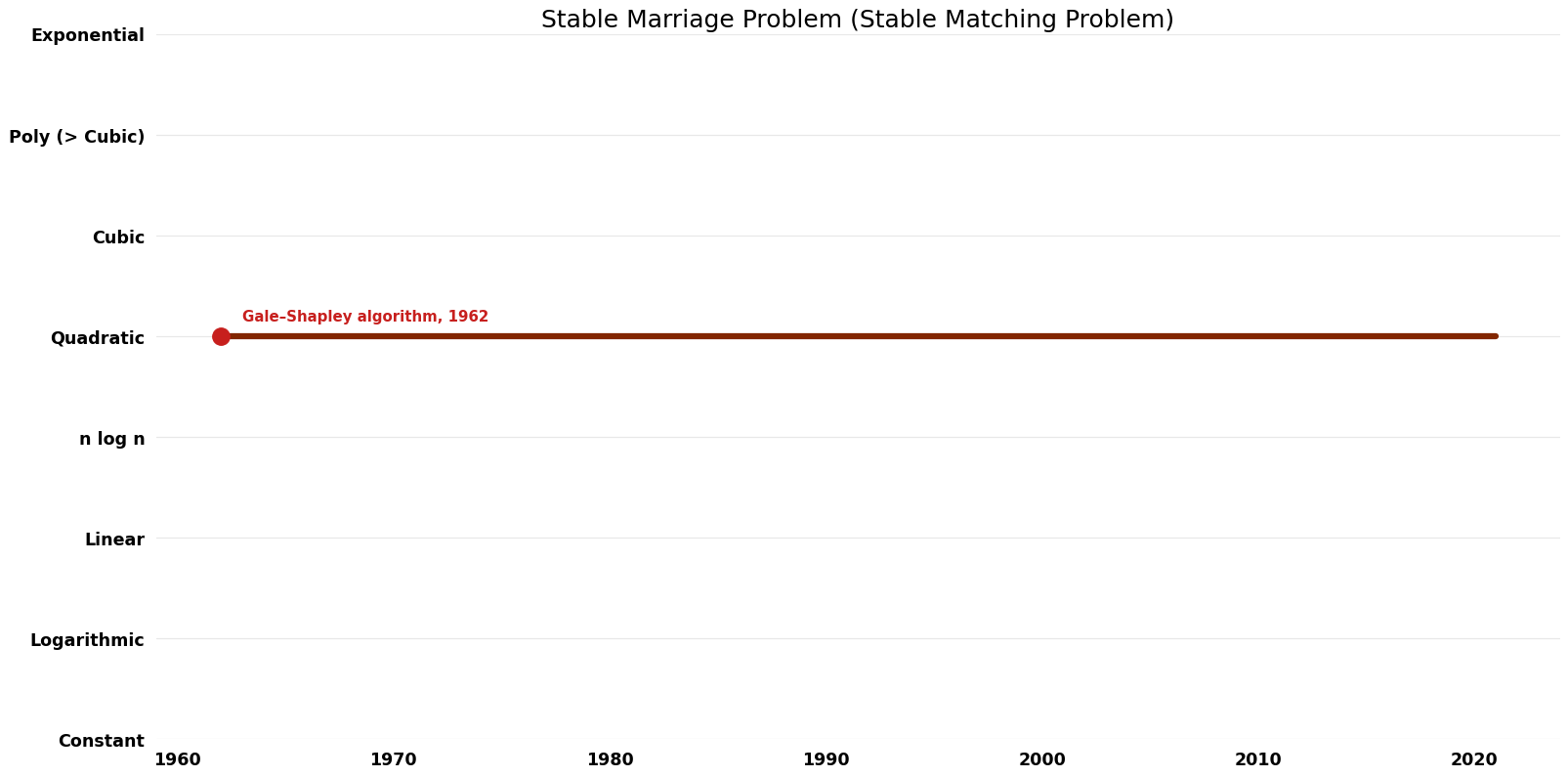
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Valentin Polishchuk, and Jukka Suomela | 2008 | $O({1})$ | $O({1})$ | 2 + \epsilon | Parallel | Time |
| Gale–Shapley algorithm | 1962 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | Time |
| Manlove; Malley | 2005 | $O(n^{2})$ | $O(n^{2})$? | Exact | Deterministic | Time |
| Unsworth; C.; Prosser; P | 2005 | $O(n^{2})$ | $O(n^{2})$? | Exact | Deterministic | Time |
| Gent; I.P.; Irving; R.W.; Manlove; D.F.; Prosser; P.; Smith; B.M. | 2001 | $O(n^{2})$ | $O(n^{2})$? | Exact | Deterministic | Time |
| S. S. TSENG and R. C. T. LEE | 1984 | $O(n^{2})$ | $O(n)$ per processor? | Exact | Parallel | Time |
| [[Tomas Feder, Nimrod Megiddoy, Serge A� Plotki (Stable Marriage Problem Stable Matching Problem)|Tomas Feder, Nimrod Megiddoy, Serge A� Plotki]] | 1994 | $O(n^{0.5})$ | $O(n^{0.5})$ auxiliary per processor? | Exact | Parallel | Time |