APSP on Dense Undirected Unweighted Graphs: Difference between revisions
(Created page with "{{DISPLAYTITLE:APSP on Dense Undirected Unweighted Graphs (All-Pairs Shortest Paths (APSP))}} == Description == In this case, the graph $G=(V,E)$ that we consider is dense ($m = O(n^2)$), is undirected, and is unweighted (or equivalently, has all unit weights). == Related Problems == Generalizations: APSP Related: APSP on Dense Directed Graphs with Arbitrary Weights, APSP on Dense Undirected Graphs with Arbitrary Weights, APSP on Geometrically Weighte...") |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
== Parameters == | == Parameters == | ||
$n$: number of vertices | |||
m: number of edges | |||
$m$: number of edges | |||
== Table of Algorithms == | == Table of Algorithms == | ||
{| class="wikitable sortable" style="text-align:center;" width="100%" | |||
== | |||
! Name !! Year !! Time !! Space !! Approximation Factor !! Model !! Reference | |||
|- | |||
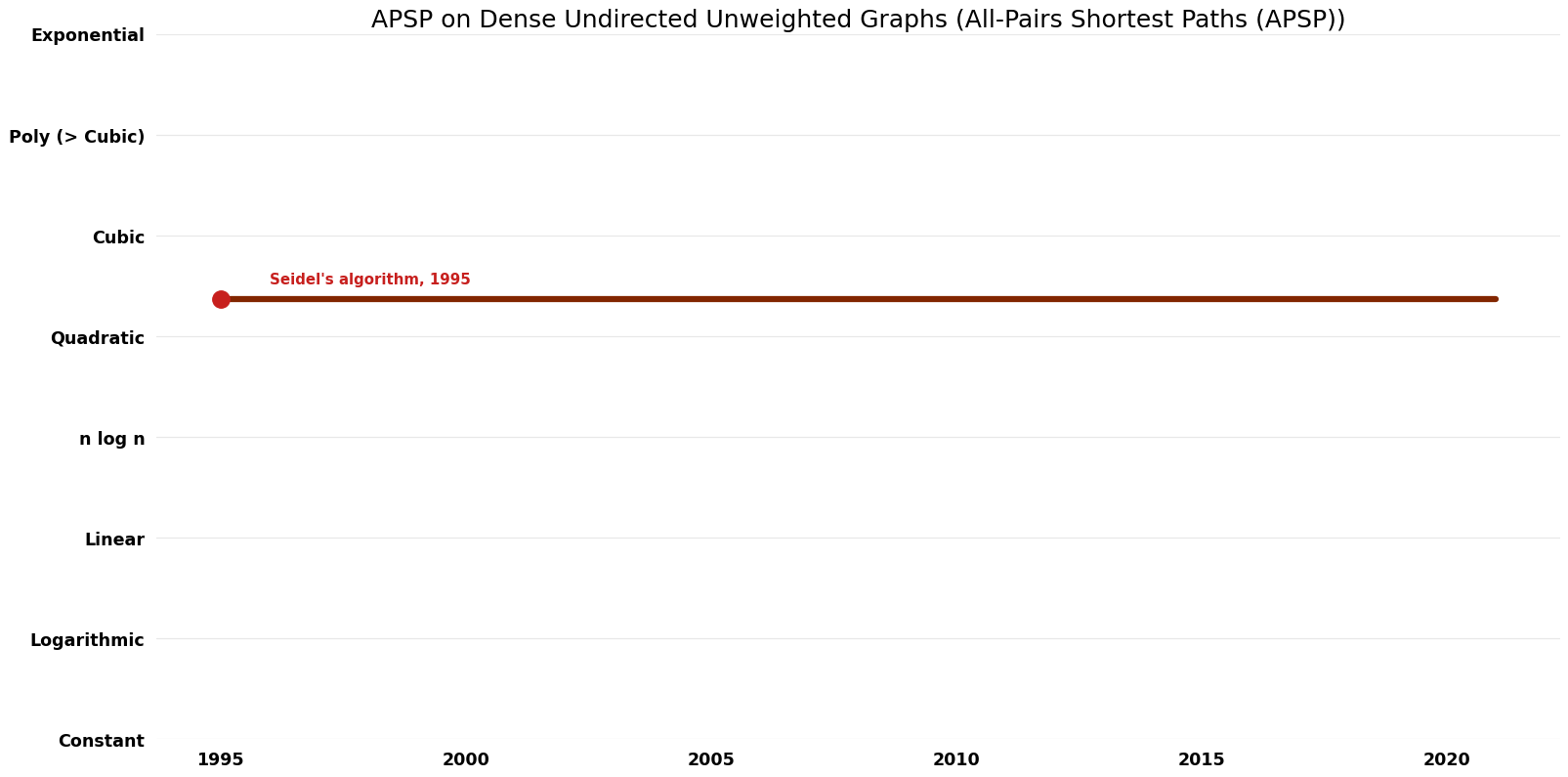
[[ | | [[Seidel's algorithm (APSP on Dense Undirected Unweighted Graphs; APSP on Sparse Undirected Unweighted Graphs All-Pairs Shortest Paths (APSP))|Seidel's algorithm]] || 1995 || $O (n^{2.{37}3} \log n)$ || $O(n^{2})$ || Exact || Deterministic || [https://www.sciencedirect.com/science/article/pii/S0022000085710781 Time] | ||
|- | |||
|} | |||
== | == Time Complexity Graph == | ||
[[File:All-Pairs Shortest Paths (APSP) - APSP on Dense Undirected Unweighted Graphs - | [[File:All-Pairs Shortest Paths (APSP) - APSP on Dense Undirected Unweighted Graphs - Time.png|1000px]] | ||
Latest revision as of 09:07, 28 April 2023
Description
In this case, the graph $G=(V,E)$ that we consider is dense ($m = O(n^2)$), is undirected, and is unweighted (or equivalently, has all unit weights).
Related Problems
Generalizations: APSP
Related: APSP on Dense Directed Graphs with Arbitrary Weights, APSP on Dense Undirected Graphs with Arbitrary Weights, APSP on Geometrically Weighted Graphs, APSP on Dense Undirected Graphs with Positive Integer Weights, APSP on Sparse Directed Graphs with Arbitrary Weights, APSP on Sparse Undirected Graphs with Positive Integer Weights, APSP on Sparse Undirected Graphs with Arbitrary Weights, APSP on Dense Directed Unweighted Graphs, APSP on Sparse Directed Unweighted Graphs, APSP on Sparse Undirected Unweighted Graphs, (5/3)-approximate ap-shortest paths
Parameters
$n$: number of vertices
$m$: number of edges
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Seidel's algorithm | 1995 | $O (n^{2.{37}3} \log n)$ | $O(n^{2})$ | Exact | Deterministic | Time |
Time Complexity Graph
_-_APSP_on_Dense_Undirected_Unweighted_Graphs_-_Time.png)