De Novo Genome Assembly: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:De Novo Genome Assembly (De Novo Genome Assembly)}} == Description == De novo sequencing refers to sequencing a novel genome where there is no reference sequence available for alignment. Sequence reads are assembled as contigs, and the coverage quality of de novo sequence data depends on the size and continuity of the contigs (ie, the number of gaps in the data). == Parameters == No parameters found. == Table of Algorithms == {| class="wikitable so...") |
No edit summary |
||
| Line 30: | Line 30: | ||
|} | |} | ||
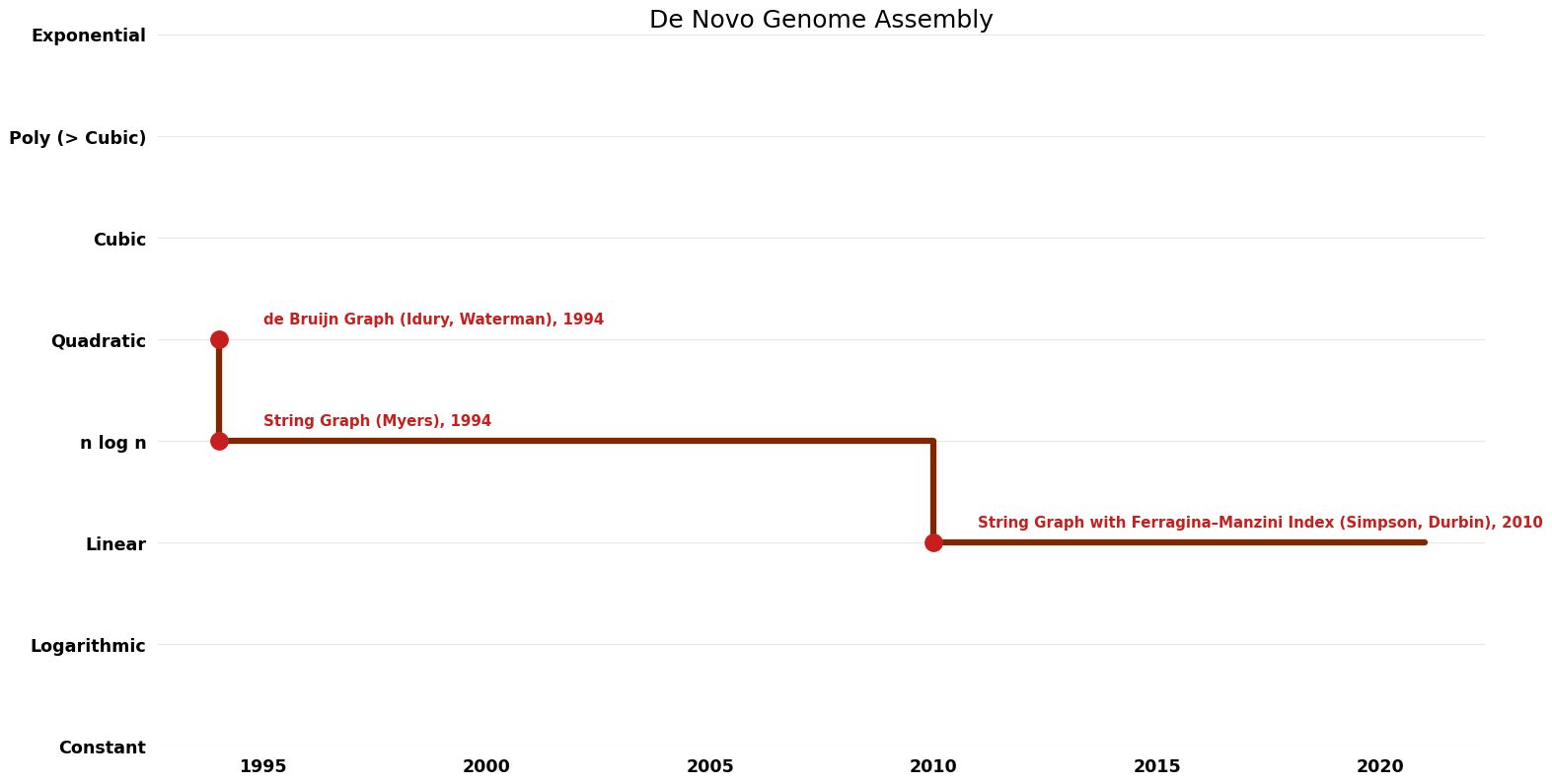
== Time Complexity | == Time Complexity Graph == | ||
[[File:De Novo Genome Assembly - Time.png|1000px]] | [[File:De Novo Genome Assembly - Time.png|1000px]] | ||
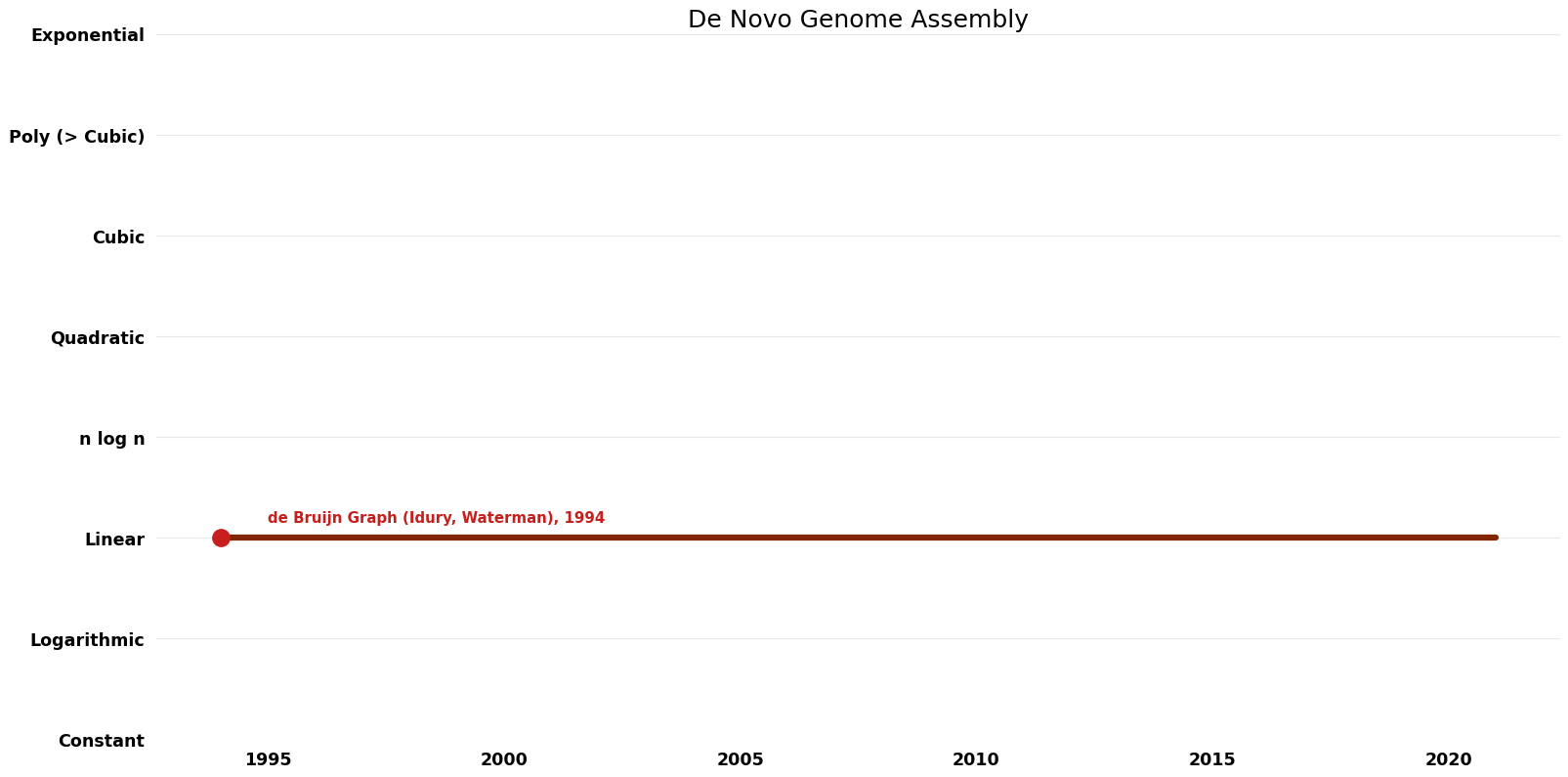
== Space Complexity | == Space Complexity Graph == | ||
[[File:De Novo Genome Assembly - Space.png|1000px]] | [[File:De Novo Genome Assembly - Space.png|1000px]] | ||
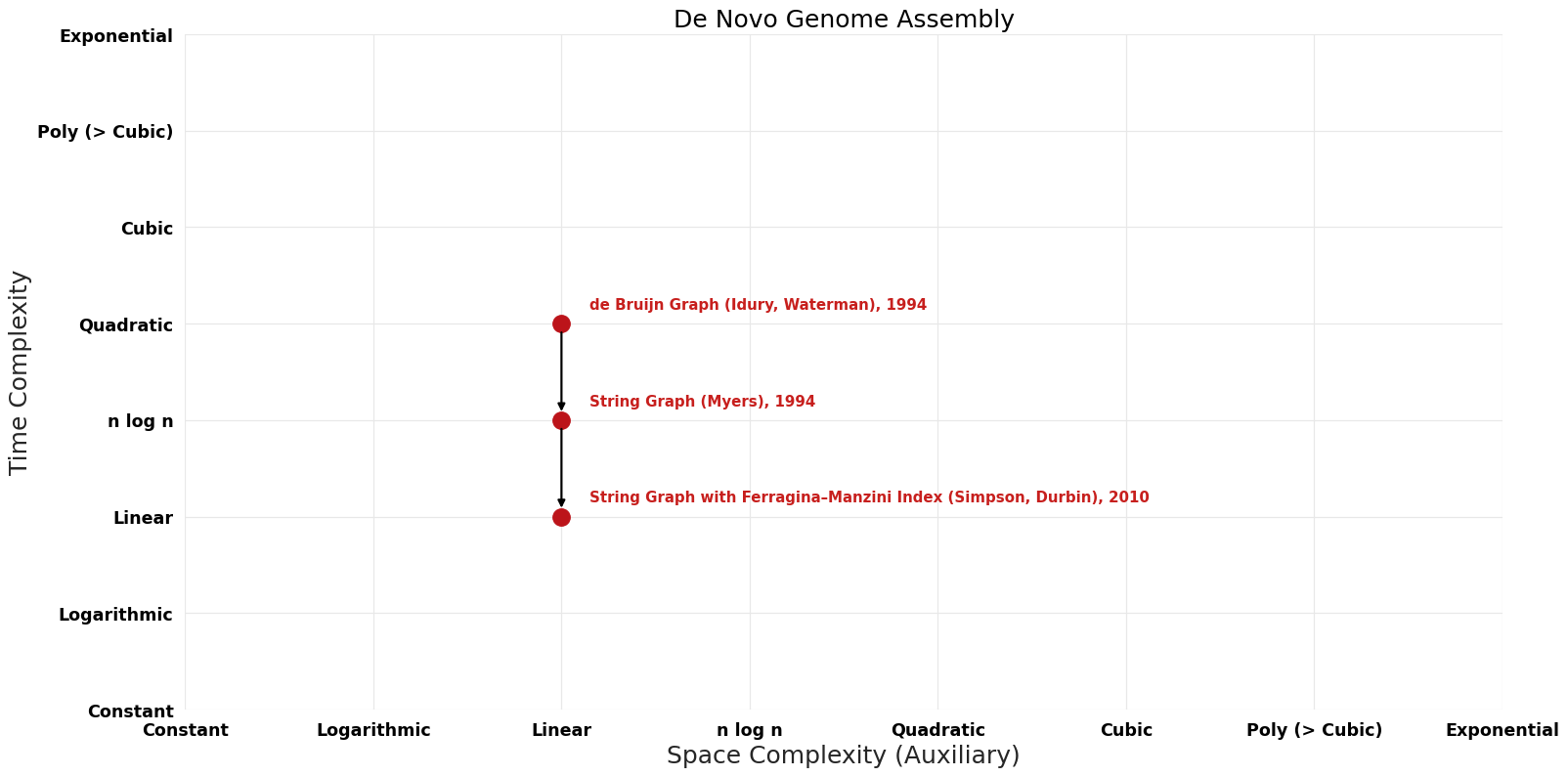
== Pareto | == Pareto Frontier Improvements Graph == | ||
[[File:De Novo Genome Assembly - Pareto Frontier.png|1000px]] | [[File:De Novo Genome Assembly - Pareto Frontier.png|1000px]] | ||
Revision as of 14:04, 15 February 2023
Description
De novo sequencing refers to sequencing a novel genome where there is no reference sequence available for alignment. Sequence reads are assembled as contigs, and the coverage quality of de novo sequence data depends on the size and continuity of the contigs (ie, the number of gaps in the data).
Parameters
No parameters found.
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Overlap Layout Consensus | 1987 | $O(n^{2})$ | $O(n^{2})$? | Deterministic | ||
| Greedy SEQAID | 1984 | $O(n^{2})$? | $O(n^{2})$? | Deterministic | Time | |
| de Bruijn Graph (Idury, Waterman) | 1994 | $O(n^{2})$ | $O(n)$? | Exact | Deterministic | Time |
| String Graph (Myers) | 1994 | $O(nlogn)$ | $O(n)$? | Exact | Deterministic | Time |
| String Graph with Ferragina–Manzini Index (Simpson, Durbin) | 2010 | $O(n)$ | $O(n)$? | Exact | Deterministic | Time |
| Hybrid Algorithm | 1999 | $O(n^{2})$ | Exact | Deterministic |