Polynomial Interpolation

Description

Given a finite number of points $x_1, \ldots , x_n$, some real constants $y_1, \ldots , y_n$ and a subspace $V$ of $\Pi^d$, find a polynomial $p \in V$, such that

$p(x_j) = y_j$, $j = 1, ... , n$

Parameters

n: number of points

d: dimension of space

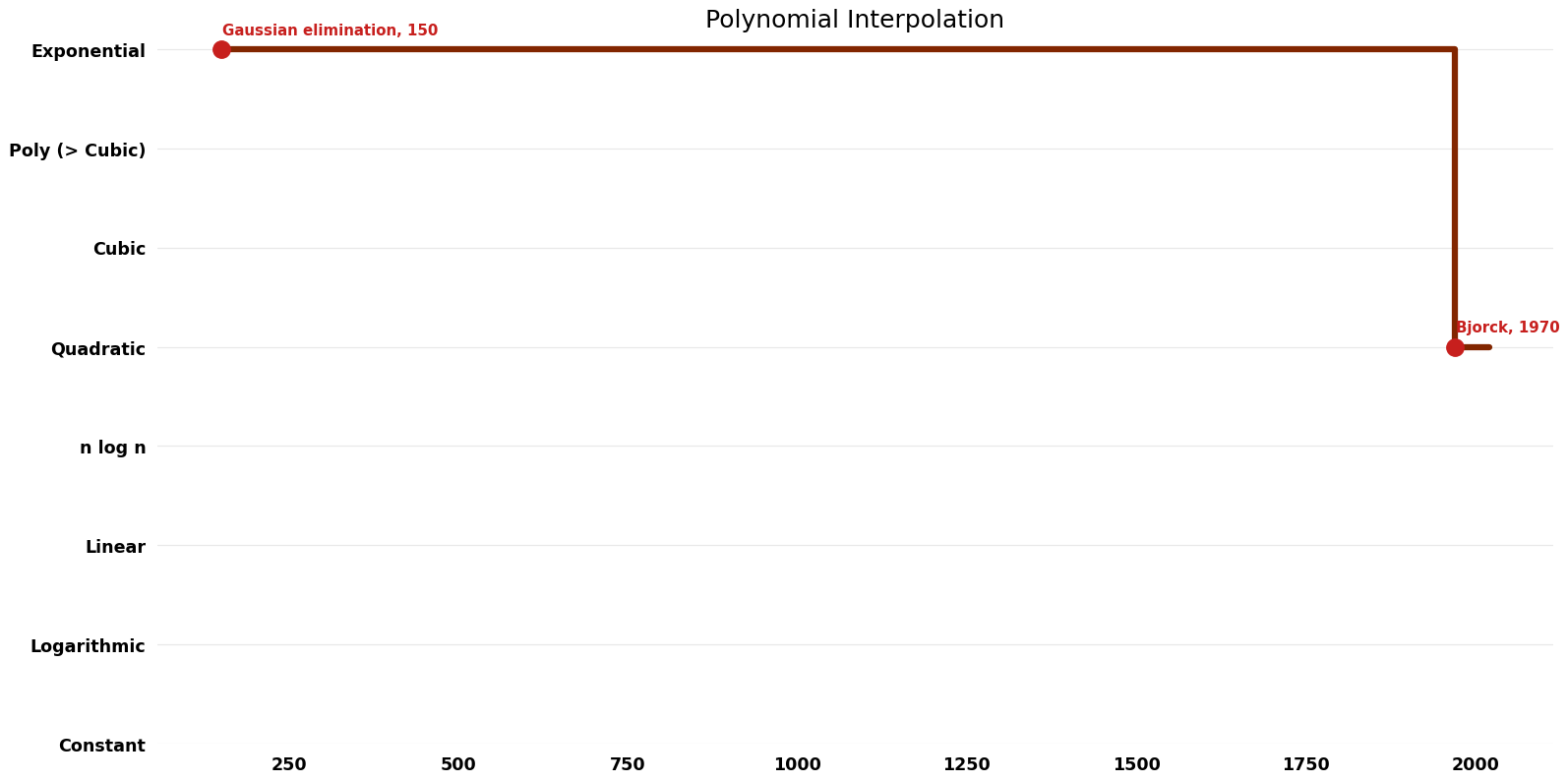
Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
Gaussian elimination	-150	$O(n^{3})$	$O(n^{2})$	Exact	Deterministic
Bjorck	1970	$O(n^{2})$	$O(n)$	Exact	Deterministic	Time & Space
Higham	1988	$O(n^{2})$	$O(n)$	Exact	Deterministic	Time & Space
Calvetti, Reichel	1993	$O(n^{2})$	$O(n)$?	Exact	Deterministic	Time

Time Complexity Graph

Space Complexity Graph

Time-Space Tradeoff