Cardinality Estimation: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
N: number of values in multiset | $N$: number of values in multiset | ||
n: cardinality of multiset (not known) | $n$: cardinality of multiset (not known) | ||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 33: | Line 33: | ||
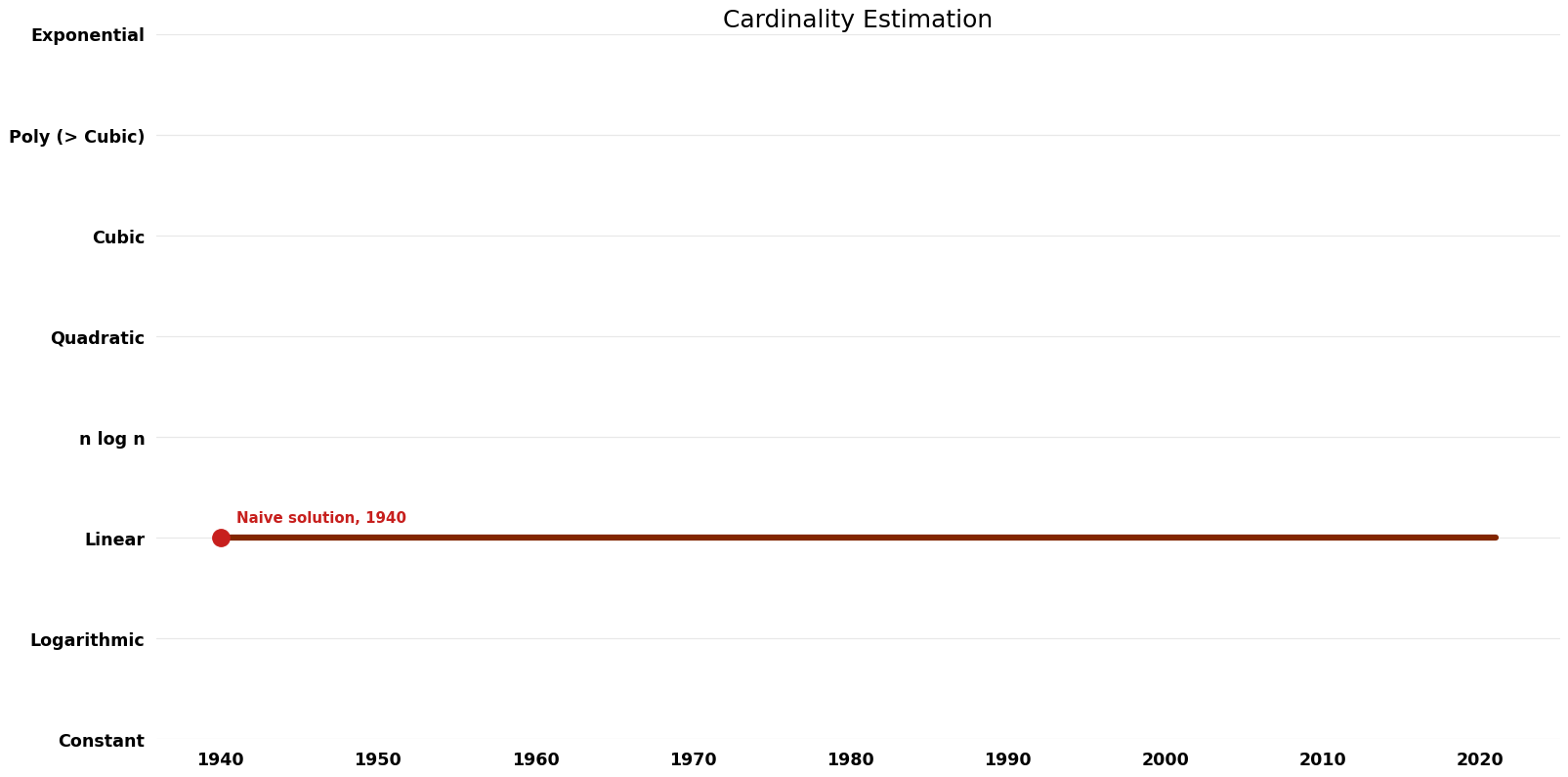
[[File:Cardinality Estimation - Time.png|1000px]] | [[File:Cardinality Estimation - Time.png|1000px]] | ||
Latest revision as of 09:08, 28 April 2023
Description
Given a multiset of (possibly hashed) values, estimate the number of distinct elements of the multiset. Of interest is minimizing storage usage.
Parameters
$N$: number of values in multiset
$n$: cardinality of multiset (not known)
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Naive solution | 1940 | $O(N)$ | $O(n)$ | Exact | Deterministic | |
| Flajolet–Martin algorithm | 1984 | $O(N)$ | $O(log n)$ | Randomized | Time & Space | |
| LogLog algorithm | 2003 | $O(N)$ | $O(log(log(n)$)) | Randomized | Time & Space | |
| HyperLogLog algorithm | 2007 | $O(N)$ | $O(eps^{-2}*log(log(n)$))+log(n)) | Randomized | Time & Space | |
| HyperLogLog++ | 2014 | $O(N)$ | $O(eps^{-2}*log(log(n)$))+log(n)) | Randomized | Time |