2-Dimensional Poisson Problem (Poisson Problem)
(Redirected from Two-dimensional elliptic partial differential equations)
Jump to navigation
Jump to search
Description
Given $f$, solve for $u$ in the 2-dimensional Poisson equation:
$u_{xx} + u_{yy} = f(x,y)$
Related Problems
Related: 3-Dimensional Poisson Problem
Parameters
$n$: dimension of grid (where grid is discretized)
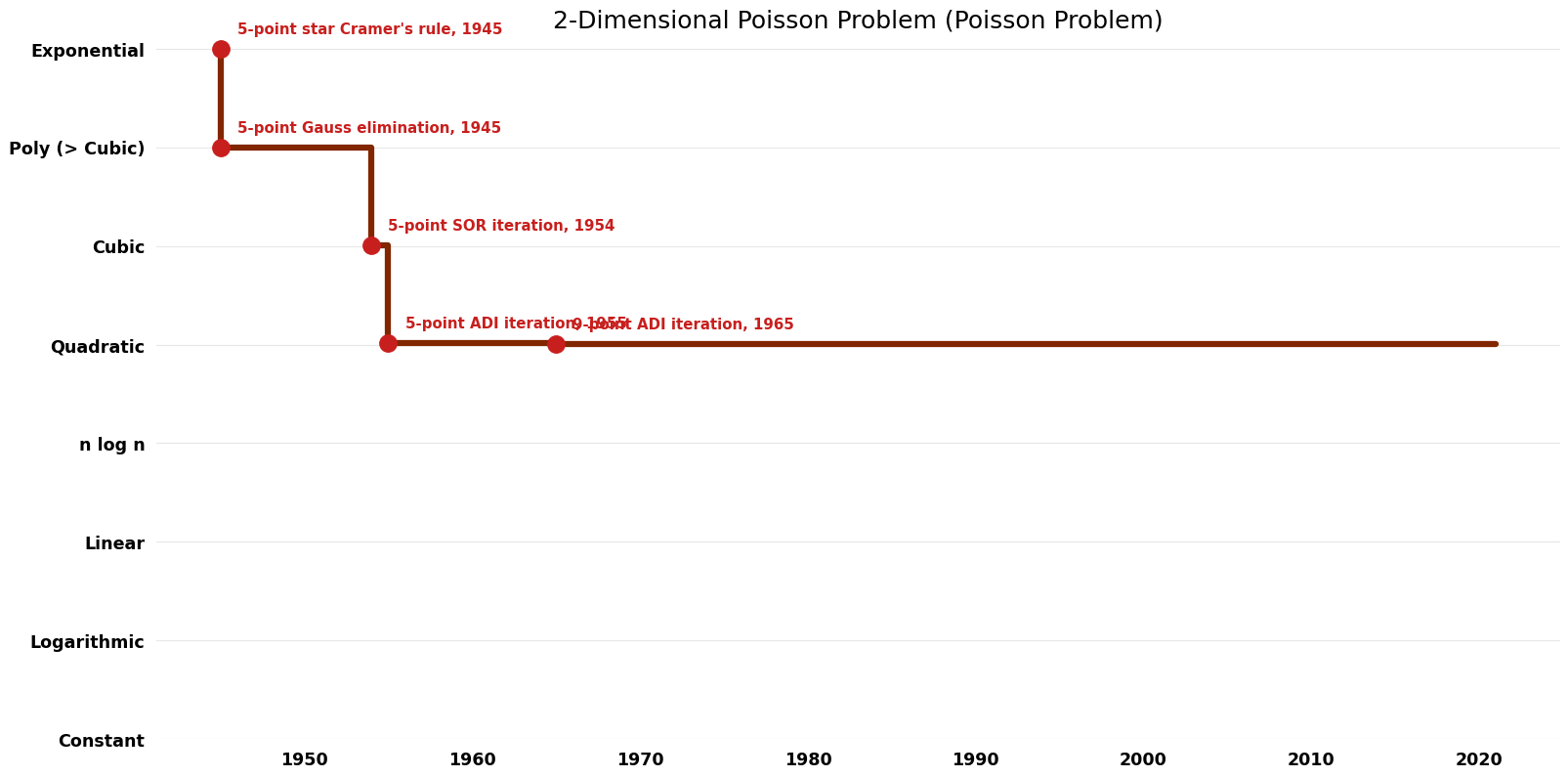
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| 5-point star Cramer's rule | 1945 | $O({4}^{(n^{2})})$ | $O({4}^{(n^{2})})$ for sure, $O(n^{2})$ possibly??? (if super conservative) | Exact | Deterministic | |
| 5-point Gauss elimination | 1945 | $O(n^{4})$ | $O(n^{4})$ | Exact | Deterministic | |
| 5-point Gauss Seidel iteration | 1945 | $O(n^{4} \log n)$ | $O(n^{2})$? | Exact | Deterministic | |
| 5-point SOR iteration | 1954 | $O(n^{3} \log n)$ | $O(n^{2})$? | Exact | Deterministic | |
| 5-point ADI iteration | 1955 | $O(n^{2} \log^{2} n)$ | $O(n^{2})$? | Exact | Deterministic | |
| 9-point SOR iteration | 1956 | $O(n^{3})$ | $O(n^{2})$? | Exact | Deterministic | |
| 9-point Tensor product | 1964 | $O(n^{3})$ | $O(n^{2})$? | Exact | Deterministic | Time |
| 9-point ADI iteration | 1965 | $O(n^{2} \log n)$ | $O(n^{2})$? | Exact | Deterministic | |
| 5-point FFT | 1965 | $O(n^{2} \log n)$ | $O(n^{2})$? | Exact | Deterministic | |
| 9-point ADI iteration + smooth guess | 1969 | $O(n^{2} \log n)$ | $O(n^{2})$? | Exact | Deterministic | |
| 5-point cyclic reduction | 1970 | $O(n^{2} \log n)$ | $O(n^{2})$? | Exact | Deterministic | |
| 9-point FFT | 1978 | $O(n^{2} \log n)$ | $O(n^{2})$? | Exact | Deterministic |