Greatest Common Divisor
Revision as of 11:56, 10 October 2022 by Admin (talk | contribs) (Created page with "== Problem Description== The greatest common divisor, sometimes also called the highest common divisor (Hardy and Wright 1979, p. 20), of two positive integers a and b is the largest divisor common to a and b. For example, GCD(3,5)=1, GCD(12,60)=12, and GCD(12,90)=6. The greatest common divisor GCD(a,b,c,...) can also be defined for three or more positive integers as the largest divisor shared by all of them. Two or more positive integers that have greatest common divis...")
Problem Description
The greatest common divisor, sometimes also called the highest common divisor (Hardy and Wright 1979, p. 20), of two positive integers a and b is the largest divisor common to a and b. For example, GCD(3,5)=1, GCD(12,60)=12, and GCD(12,90)=6. The greatest common divisor GCD(a,b,c,...) can also be defined for three or more positive integers as the largest divisor shared by all of them. Two or more positive integers that have greatest common divisor 1 are said to be relatively prime to one another, often simply just referred to as being "relatively prime."
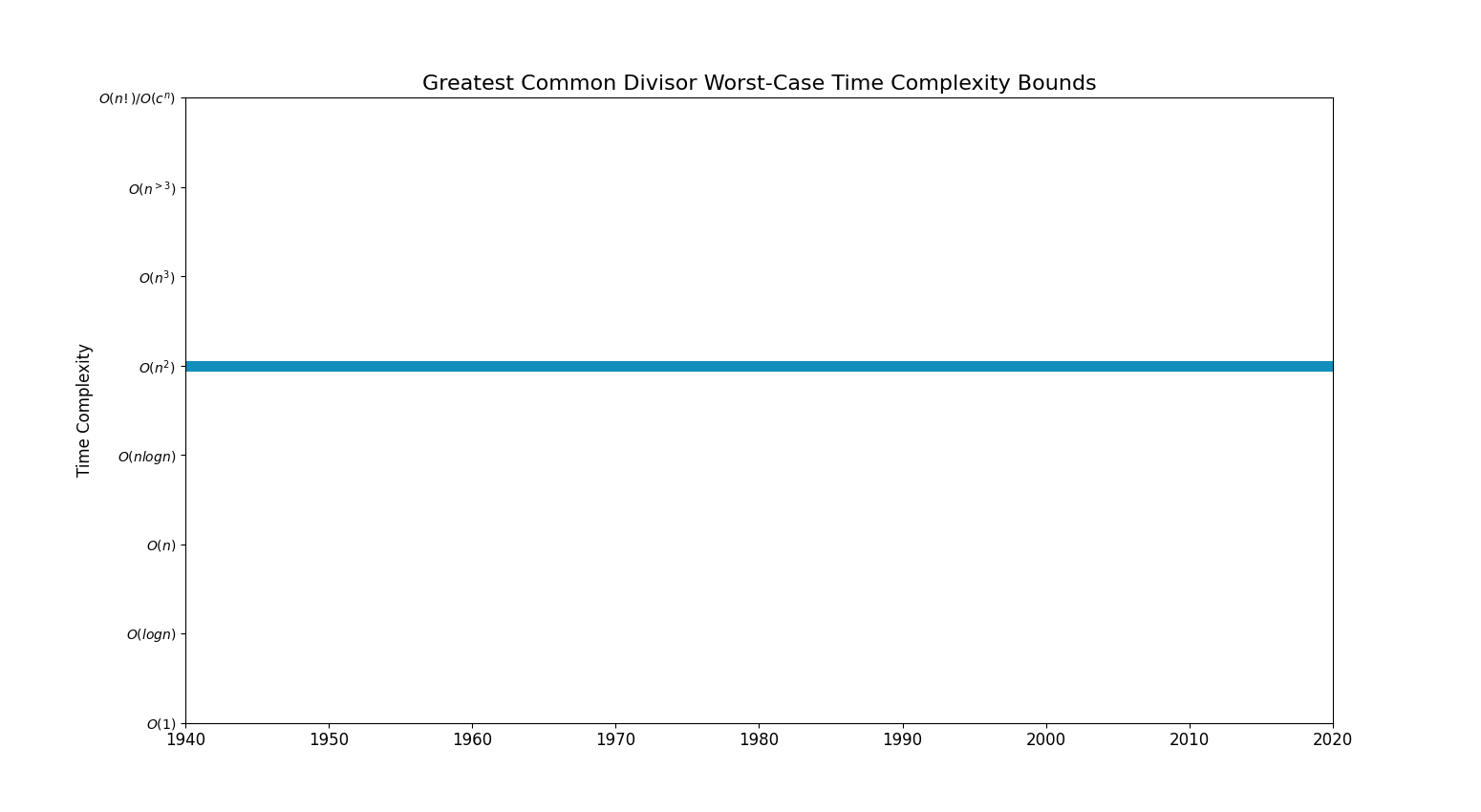
Bounds Chart
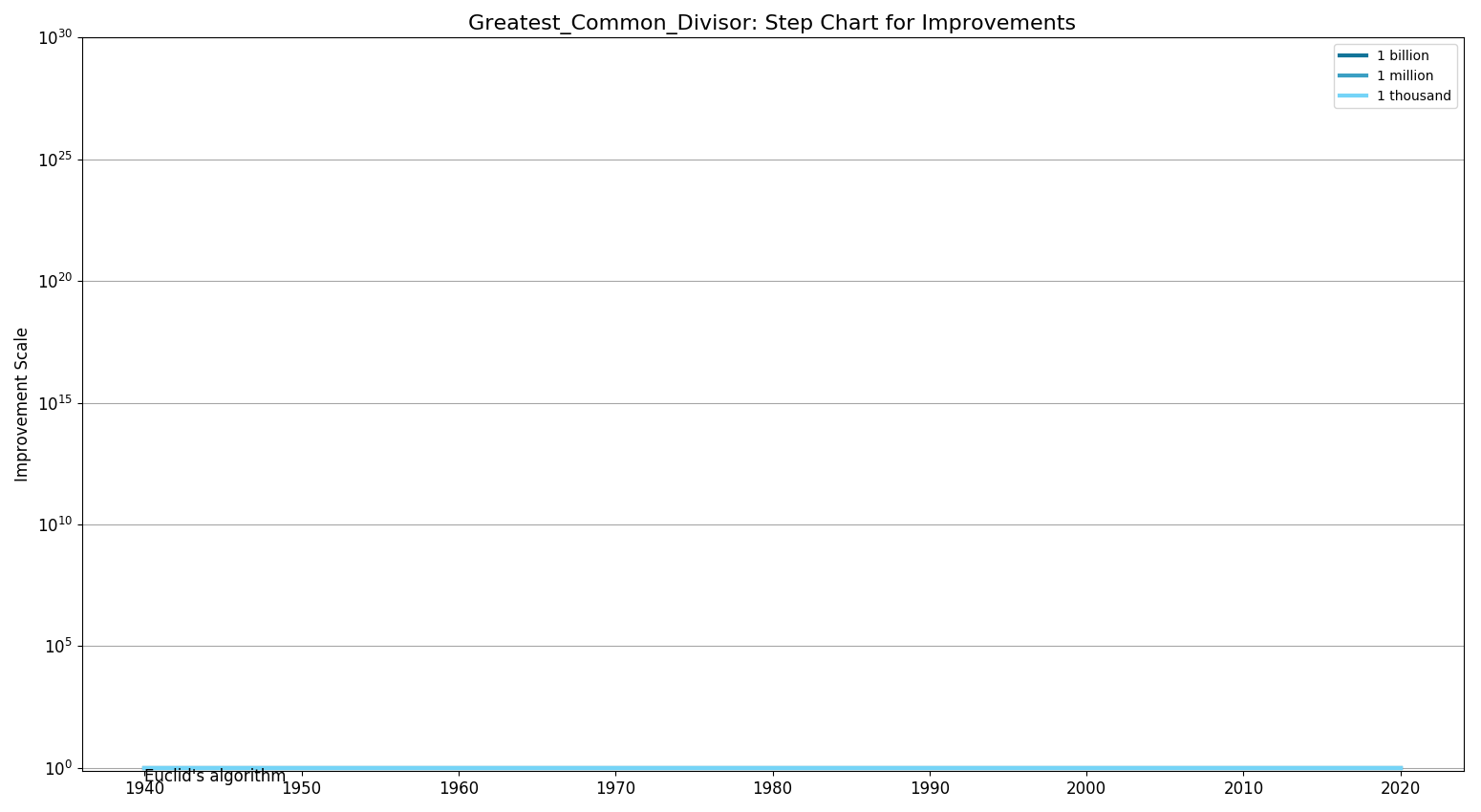
Step Chart
Improvement Table
| Complexity Classes | Algorithm Paper Links | Lower Bounds Paper Links |
|---|---|---|
| Exp/Factorial | ||
| Polynomial > 3 | ||
| Cubic | ||
| Quadratic | [ Euclid's algorithm (-300)]
[ Lehmer's GCD algorithm (1940)] [ Binary GCD algorithm (1967)] |
|
| nlogn | ||
| Linear | ||
| logn |