Lossy Compression (Data Compression)

Description

The reduction or ideally elimination of redundancies in the original data to result in smaller required storage space is the goal of every compression scheme. There are two categories of data compression: lossy and lossless.

Lossy compression is achieved by only discarding the redundancies and out of human perception information and getting rid of those extra bits.

Related Problems

Related: Lossless Compression

Parameters

$n$: number of items in input series of data

Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
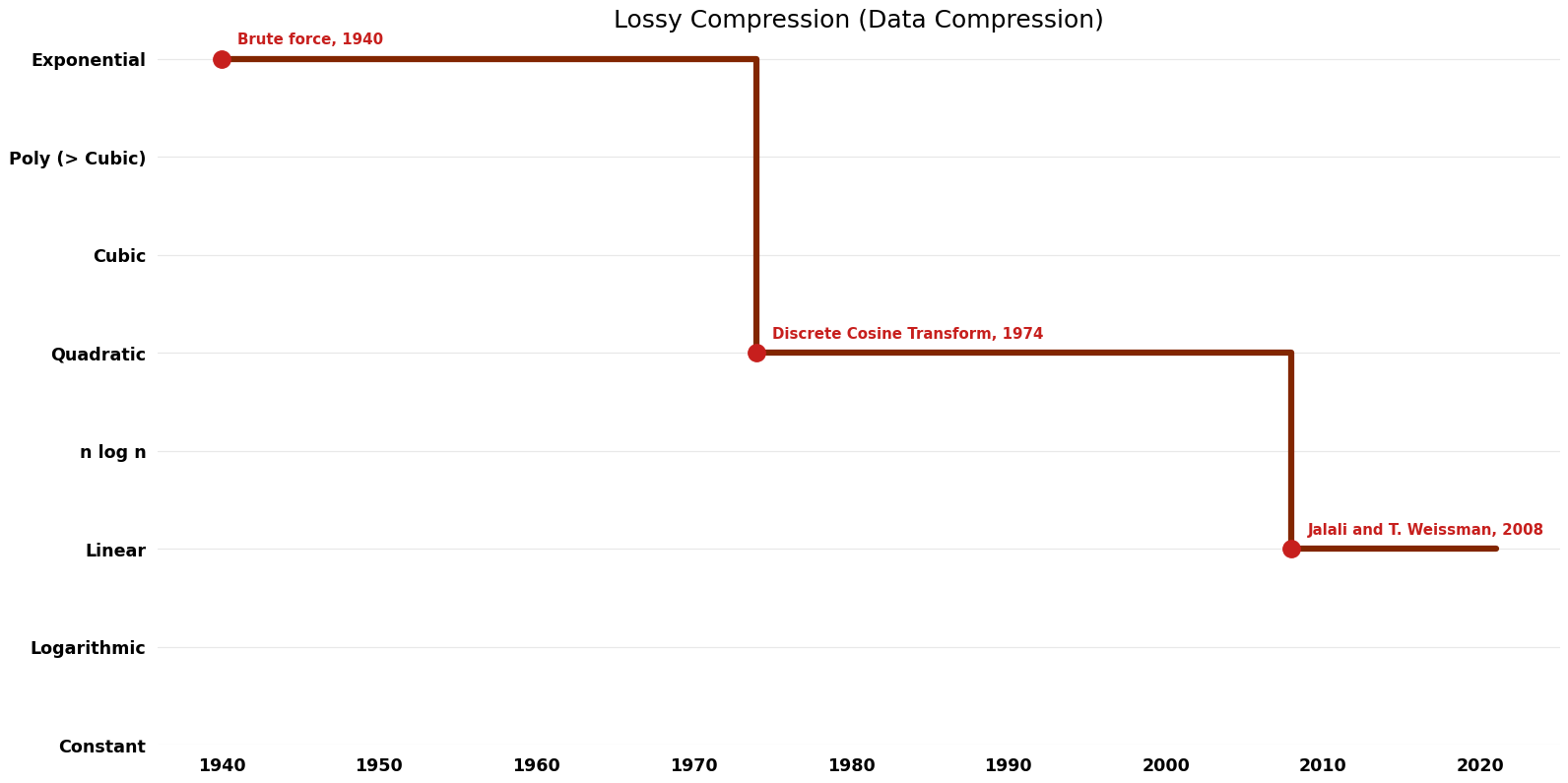
Gupta; Verdu	2009	$O(n^{2} log^{3} n)$	$O(n)$	Exact	Deterministic	Time
Discrete Cosine Transform	1974	$O(n^{2})$	$O(n)$	Exact	Deterministic	Time
Maneva and M. J. Wainwright	2005	$O(n^{2})$	$O(n^{2})$	Exact	Deterministic	Time
Ciliberti; Mézard	2005	$O(n^{2})$	$O(n^{2})$?	Exact	Deterministic	Time
Brute force	1940	$O(n*{2}^n)$	$O(n*{2}^n)$?	Exact	Deterministic
Matsunaga; Yamamoto	2003	$O(n*{2}^n)$	exp(n)	Exact	Deterministic	Time & Space
Sun; M. Shao; J. Chen; K. Wong; and X. Wu	2010	$O(kmn)$?	$O(kmn)$?	Exact	Deterministic	Time
Miyake	2006	$O(n*{2}^n)$	$O({2}^n)$	Exact	Deterministic	Time
Martinian and M. J. Wainwright	2006	$O(n*{2}^n)$	$O(mn+mk)$?	Exact	Deterministic	Time
Jalali and T. Weissman	2008	$O(n)$	$O(n)$?	Exact	Deterministic	Time
Jalali; A. Montanari; and T. Weissman	2010	$O(n)$	$O(n)$?	Exact	Deterministic	Time
Korada and R. Urbanke;	2010	$O(n*{2}^n)$	$O(N)$	Exact	Deterministic	Time

Time Complexity Graph