3-Dimensional Poisson Problem (Poisson Problem)

Description

Given $f$, solve for $u$ in the 3-dimensional Poisson equation:

$u_{xx} + u_{yy} + u_{zz} = f(x,y,z)$

$n$: dimension of grid (where grid is discretized)

Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
5-point star Cramer's rule	1945	$O({5}^{(n^{3})$})	$O({5}^{(n^{3})})$ for sure, $O(n^{3})$ possibly??? (if super conservative)	Exact	Deterministic
5-point Gauss elimination	1945	$O(n^{7})$	$O(n^{6})$	Exact	Deterministic
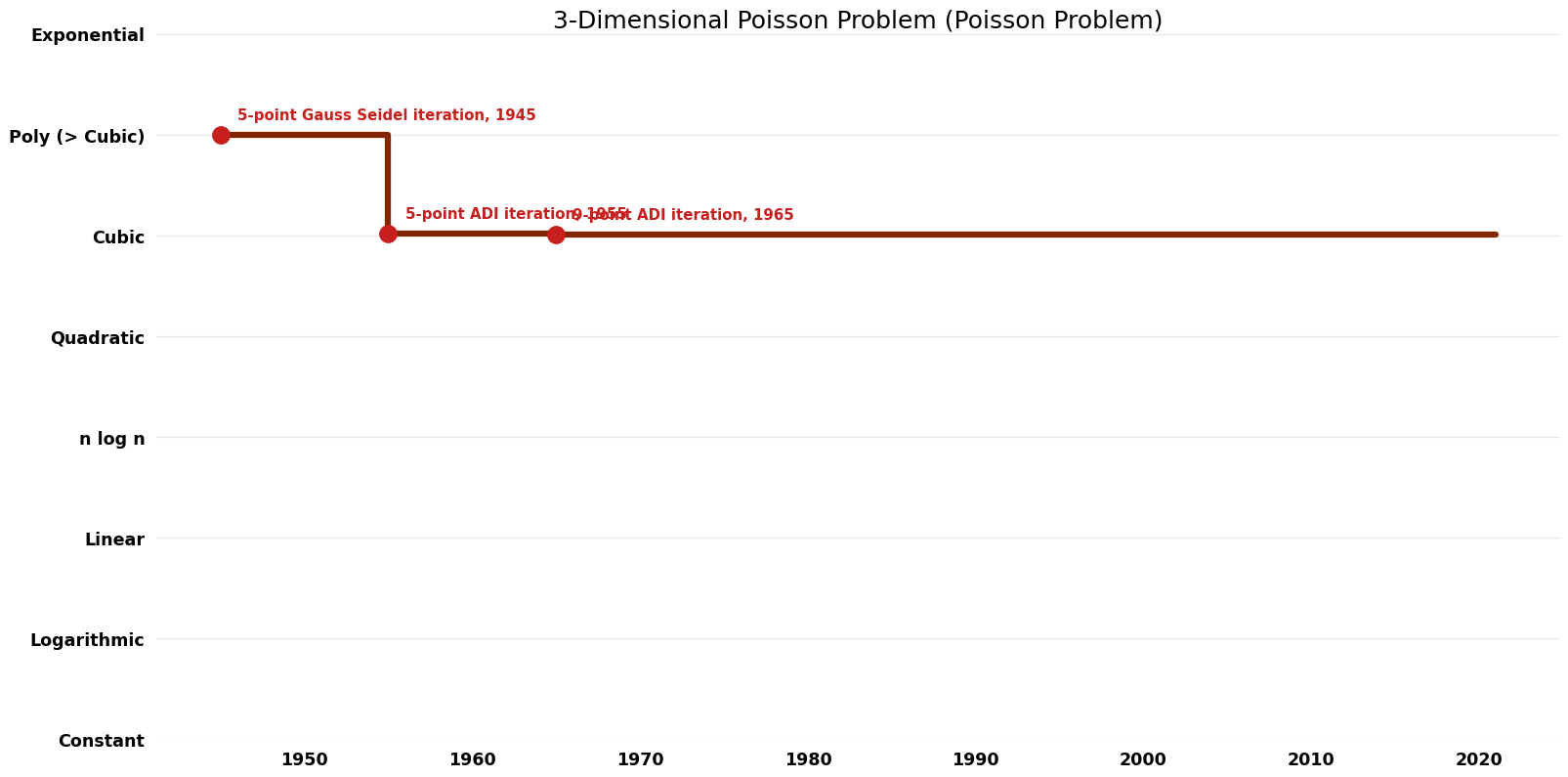
5-point Gauss Seidel iteration	1945	$O(n^{5} \log n)$	$O(n^{3})$?	Exact	Deterministic
5-point SOR iteration	1954	$O(n^{4} \log n)$	$O(n^{3})$?	Exact	Deterministic
5-point ADI iteration	1955	$O(n^{3} \log^{2} n)$	$O(n^{3})$?	Exact	Deterministic
9-point SOR iteration	1956	$O(n^{4})$	$O(n^{3})$?	Exact	Deterministic
9-point Tensor product	1964	$O(n^{4})$	$O(n^{3})$?	Exact	Deterministic	Time
9-point ADI iteration	1965	$O(n^{3} \log n)$	$O(n^{3})$?	Exact	Deterministic
5-point FFT	1965	$O(n^{3} \log n)$	$O(n^{3})$?	Exact	Deterministic
9-point ADI iteration + smooth guess	1969	$O(n^{3} \log n)$	$O(n^{3})$?	Exact	Deterministic
5-point cyclic reduction	1970	$O(n^{3} \log n)$	$O(n^{3})$?	Exact	Deterministic
9-point FFT	1978	$O(n^{3} \log n)$	$O(n^{3})$?	Exact	Deterministic