Hyperbolic Spline Interpolation (Hyperbolic Spline Interpolation)

Description

The problem of restoring complex curves and surfaces from discrete data so that their shape is preserved is called isogeometric interpolation. A very popular tool for solving this problem are hyperbolic splines in tension, which were introduced in 1966 by Schweikert. These splines have smoothness sufficient for many applications; combined with algorithms for the automatic selection of the tension parameters, they adapt well to the given data. Unfortunately, the evaluation of hyperbolic splines is a very difficult problem because of roundoff errors (for small values of the tension parameters) and overflows (for large values of these parameters).�

Parameters

$n$: number of points

Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
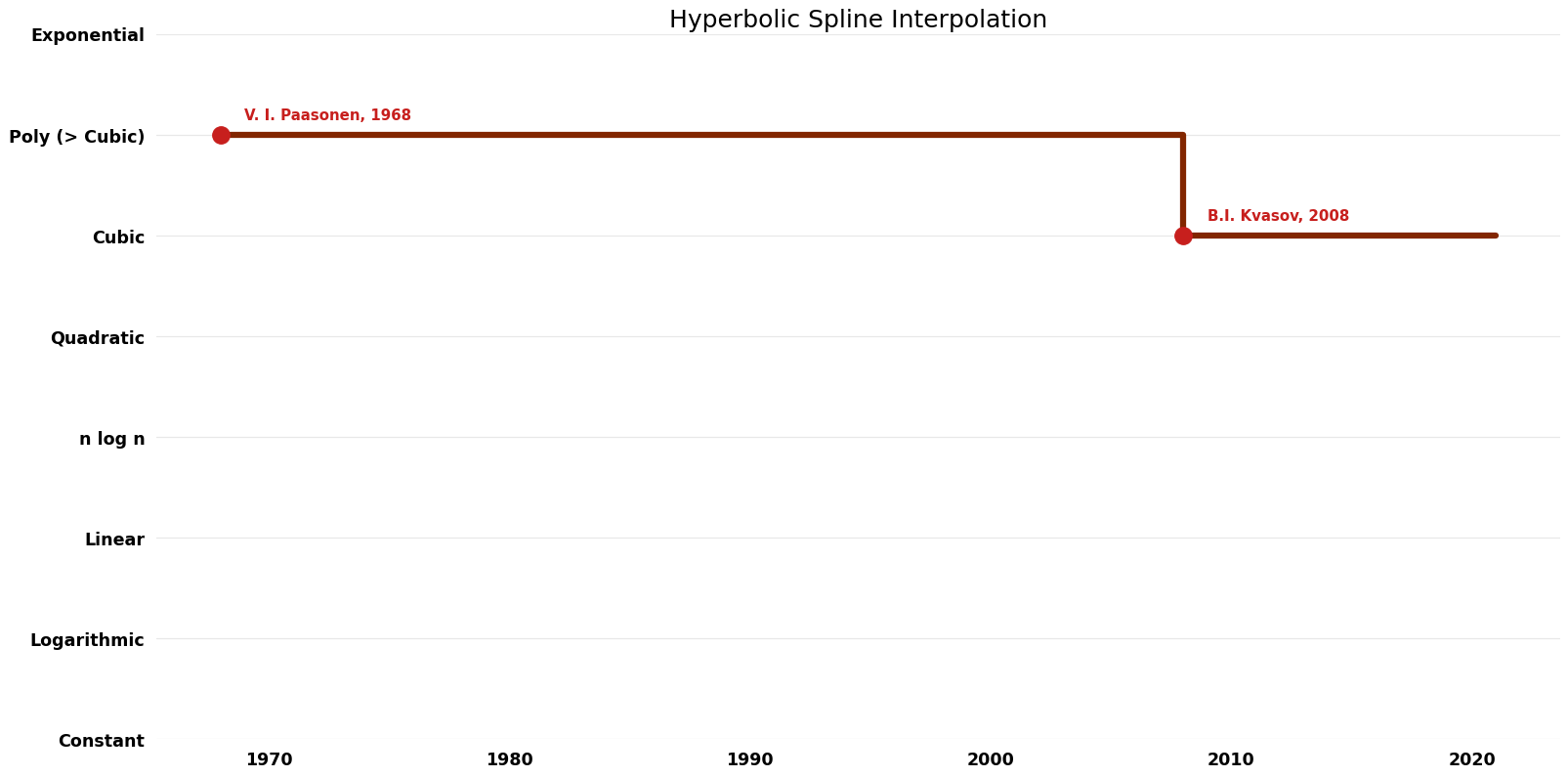
B.I. Kvasov	2008	$O(n^{3} \log^{2}K)$	$O(n)$?	Exact	Deterministic	Time
V. A. Lyul’ka and A. V. Romanenko	1994	$O(n^{5})$		Exact	Deterministic	Time
V. A. Lyul’ka and I. E. Mikhailov	2003	$O(n^{4})$		Exact	Deterministic	Time
V. I. Paasonen	1968	$O(n^{5} \log K)$		Exact	Deterministic
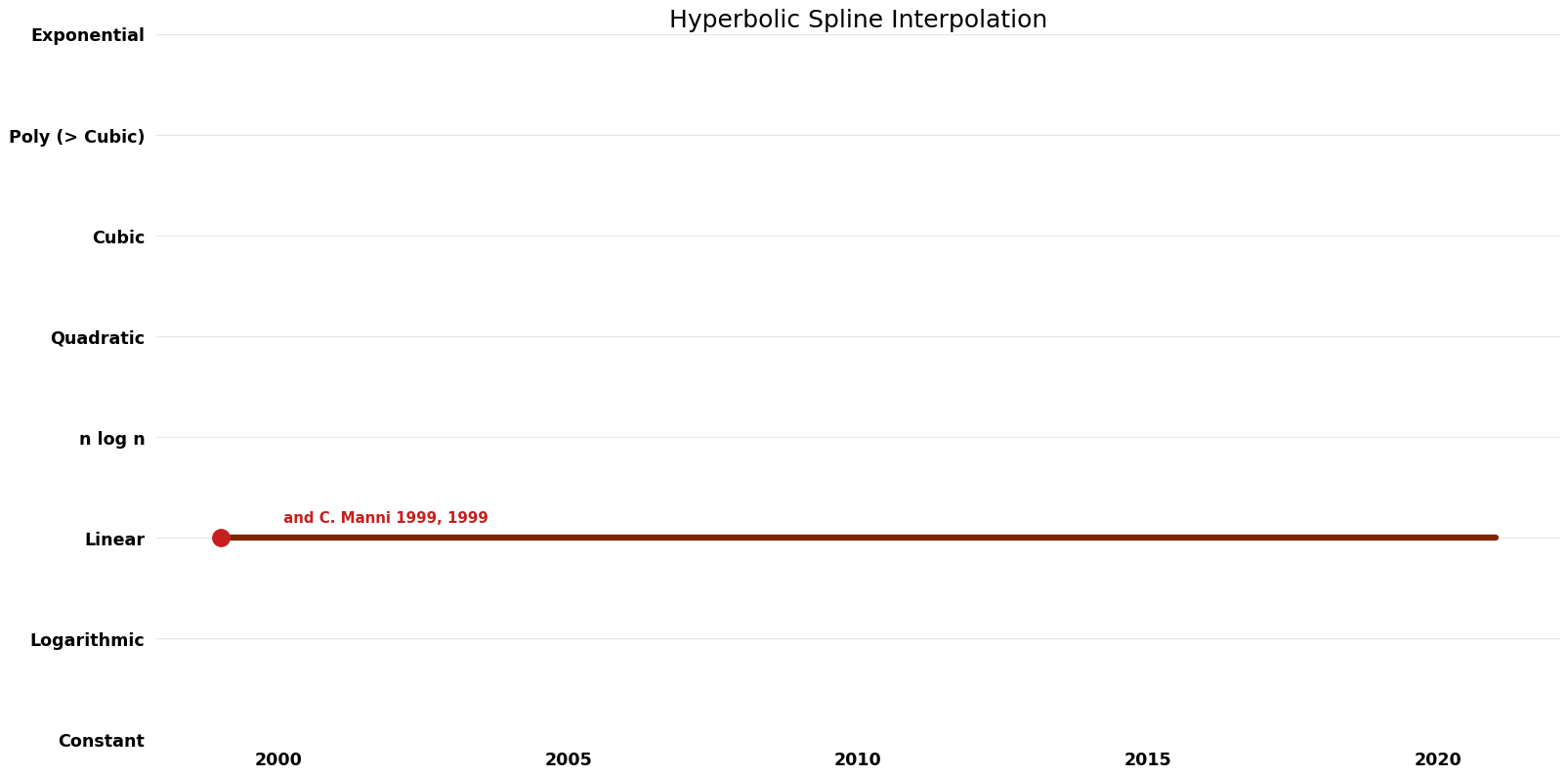
P. Costantini, B. I. Kvasov, and C. Manni	1999	$O(n^{5} \log K)$	$O(n)$?	Exact	Deterministic	Time
B. I. Kvasov	2000	$O(n^{4})$	$O(n)$??	Exact	Deterministic	Time

Time Complexity Graph

Space Complexity Graph

Time-Space Tradeoff