Decisional BCNF (BCNF Decomposition)
Jump to navigation
Jump to search
Description
Decisional BCNF is the problem of deciding whether or not a relation schema can be turned into Boyce-Codd normal form (BCNF).
A relation schema $R$ is in Boyce Codd Normal Form (abbr. BCNF) if for all non-trivial FDs $X \rightarrow Y$ in $F^+$, $X$ is a superkey. In extending this notion to database schemas, we must be conscious of the UR-assumption. We say that $R_i = <ATTR_i,F_i>$ is in BCNF if the schema $<ATTR_i, F^+(ATTR_i)>$ is in BCNF, and $D$ is in BCNF if each $R_i$ is.
Related Problems
Related: BCNF Decomposition
Parameters
No parameters found.
Table of Algorithms
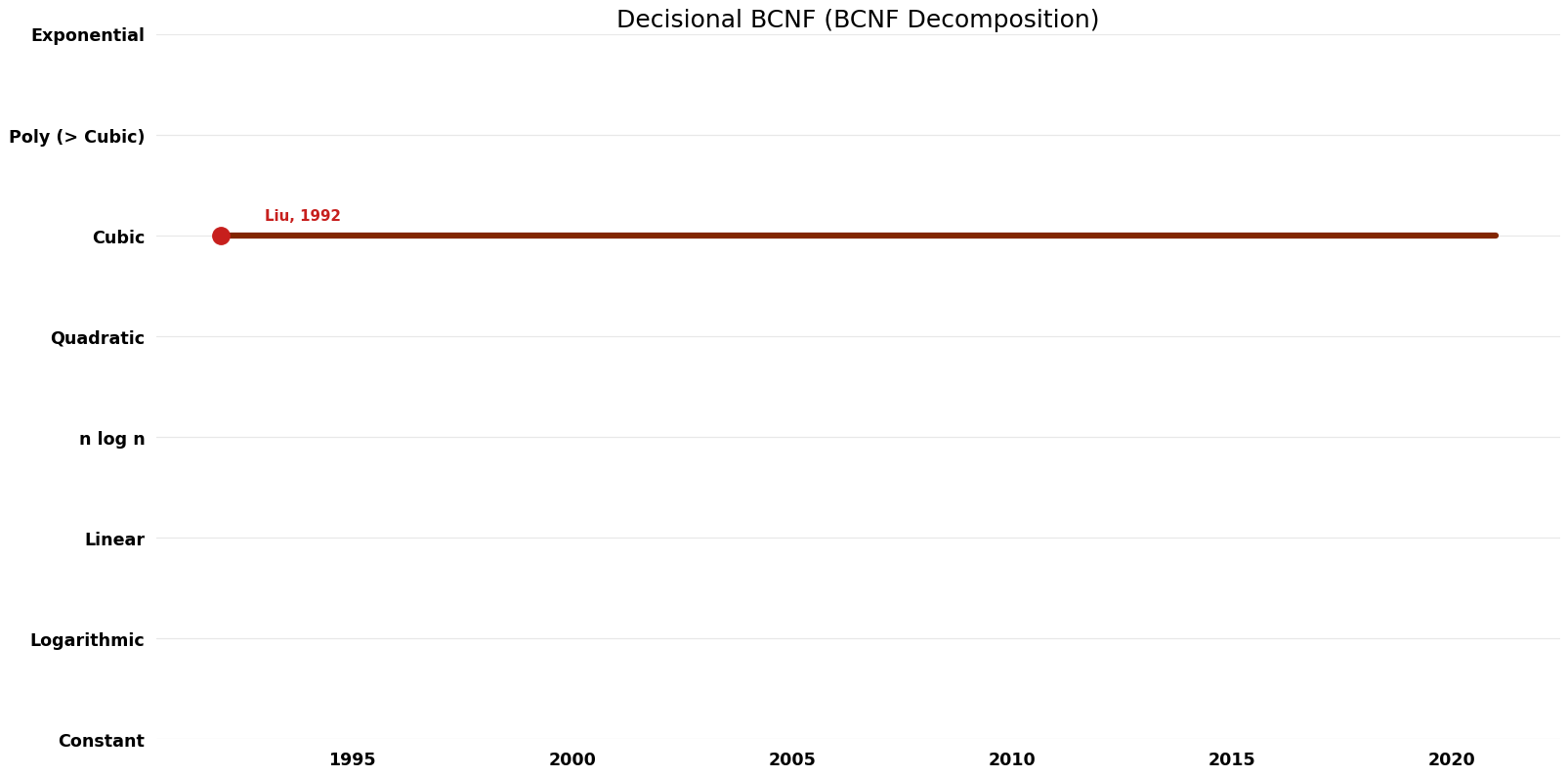
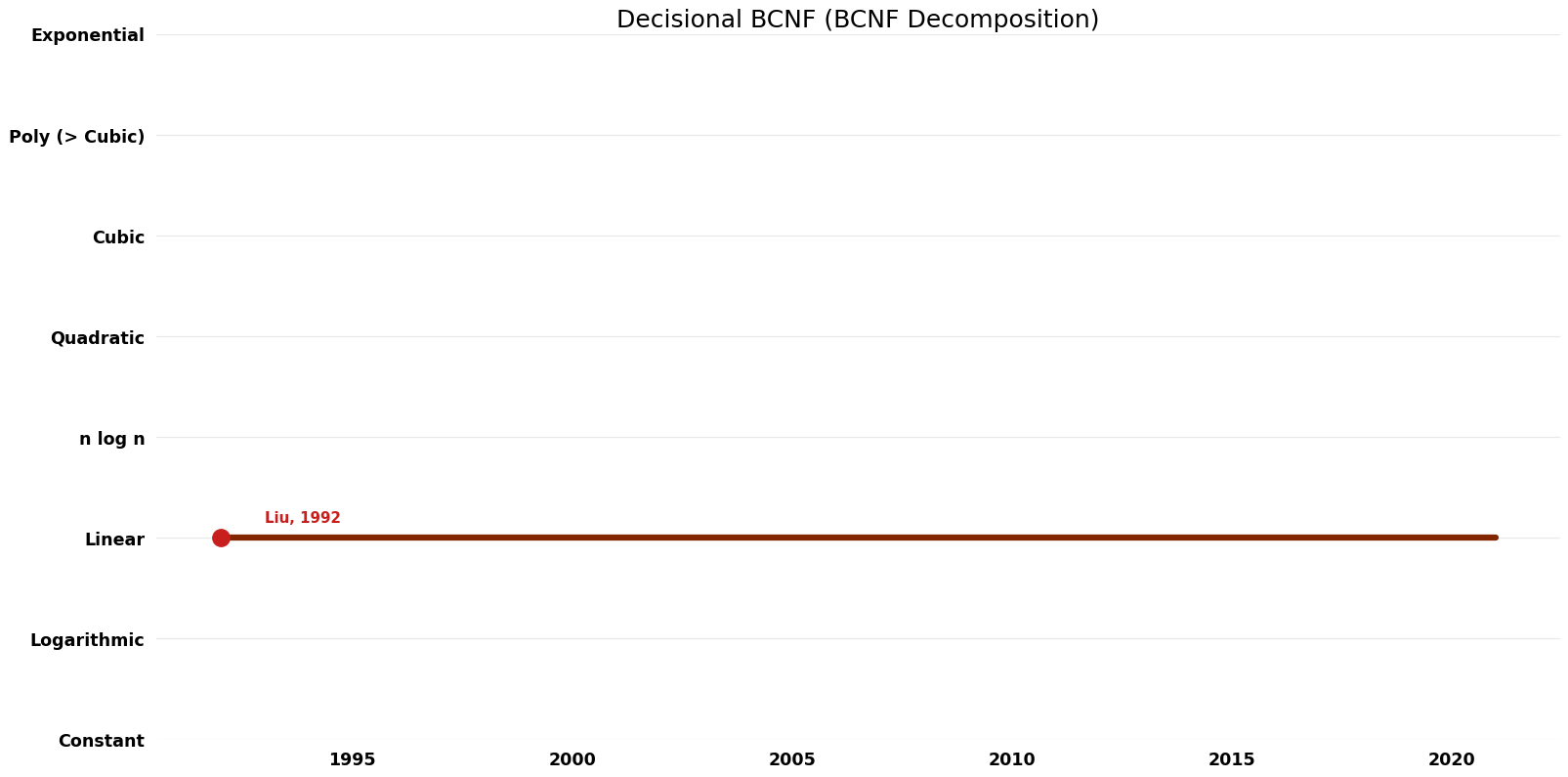
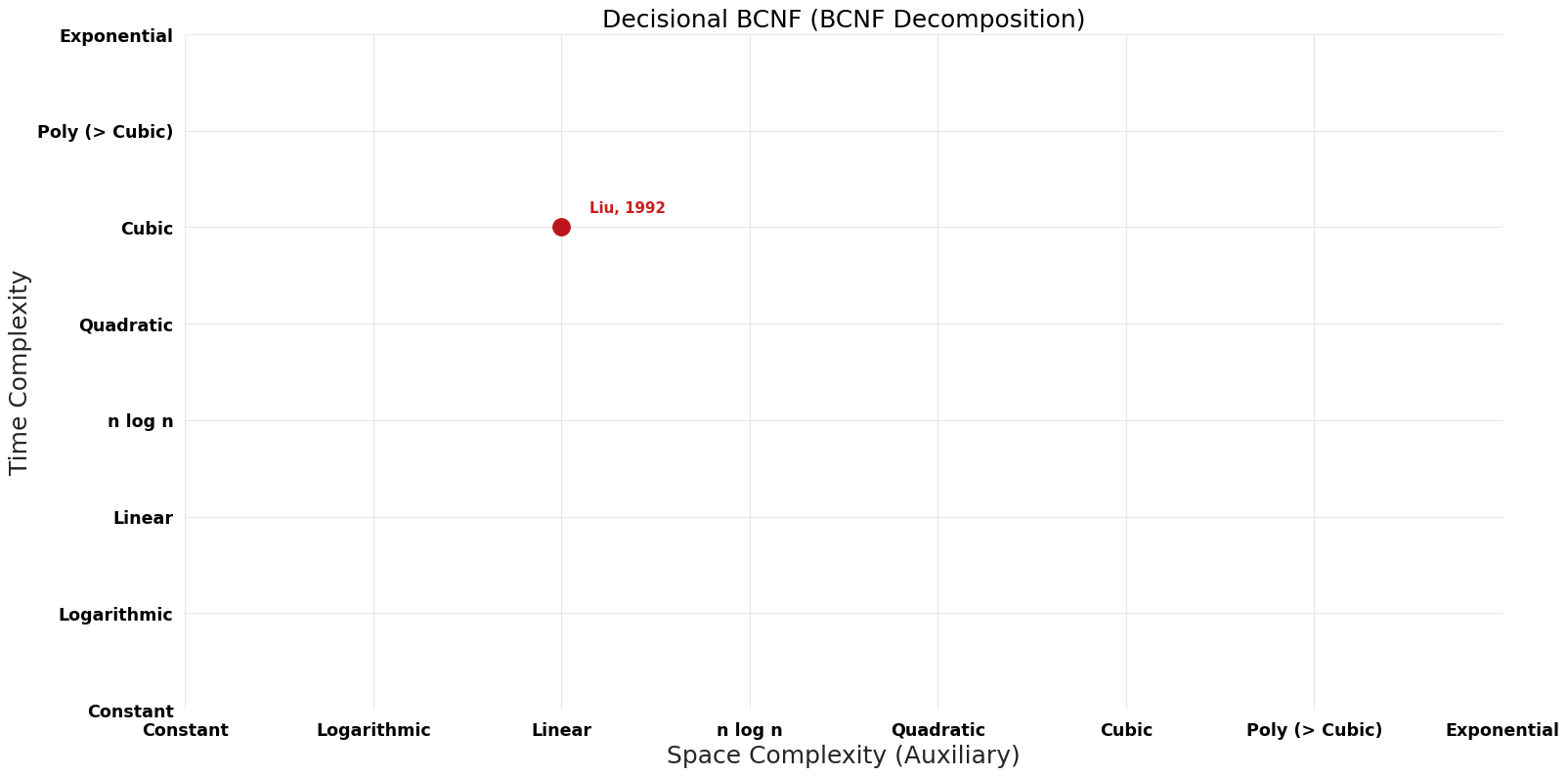
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Liu | 1992 | $O(kn^{2})$ | $O(n)$ | Exact | Deterministic | Time |
Time Complexity Graph
Space Complexity Graph
Space-Time Tradeoff Improvements
