Inexact GED (Graph Edit Distance Computation)
Jump to navigation
Jump to search
Description
The GED of two graphs is defined as the minimum cost of an edit path between them, where an edit path is a sequence of edit operations (inserting, deleting, and relabeling vertices or edges) that transforms one graph into another. Inexact GED computes an answer that is not gauranteed to be the exact GED.
Related Problems
Related: Exact GED
Parameters
V: number of vertices in the larger of the two graphs
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Y Bai | 2018 | $O(V^{2})$ | $O(V^{2})$ | none stated | Deterministic | Time |
| L Chang | 2017 | $O(V E^{2} logV)$ | $O(V)$ | Exact | Deterministic | Time & Space |
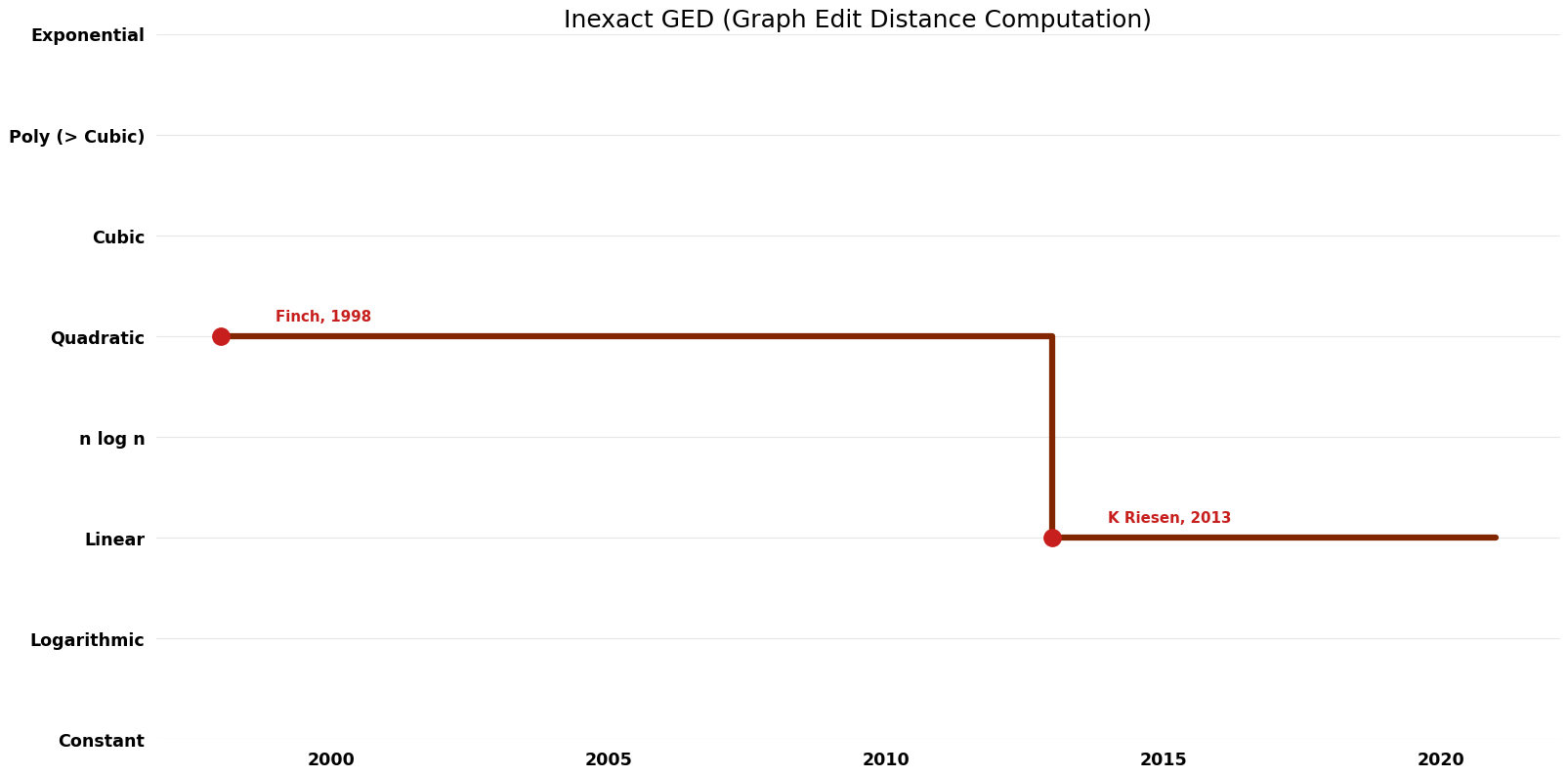
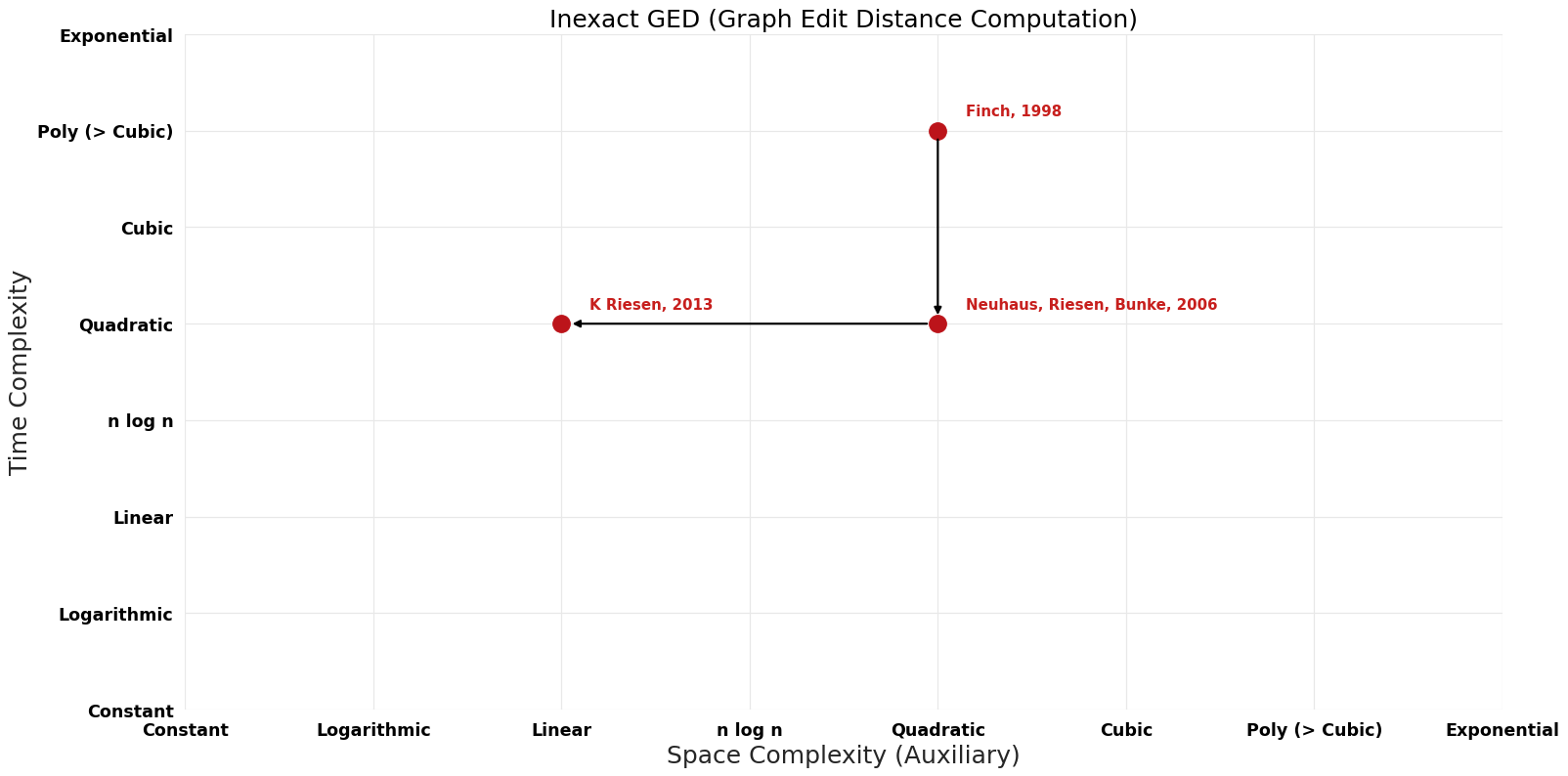
| K Riesen | 2013 | $O(V^{2})$ | $O(V)$ | Exact | Deterministic | Time |
| Alberto Sanfeliu and King-Sun Fu | 1983 | $O(V^{3} E^{2})$ | Exact | Deterministic | Time | |
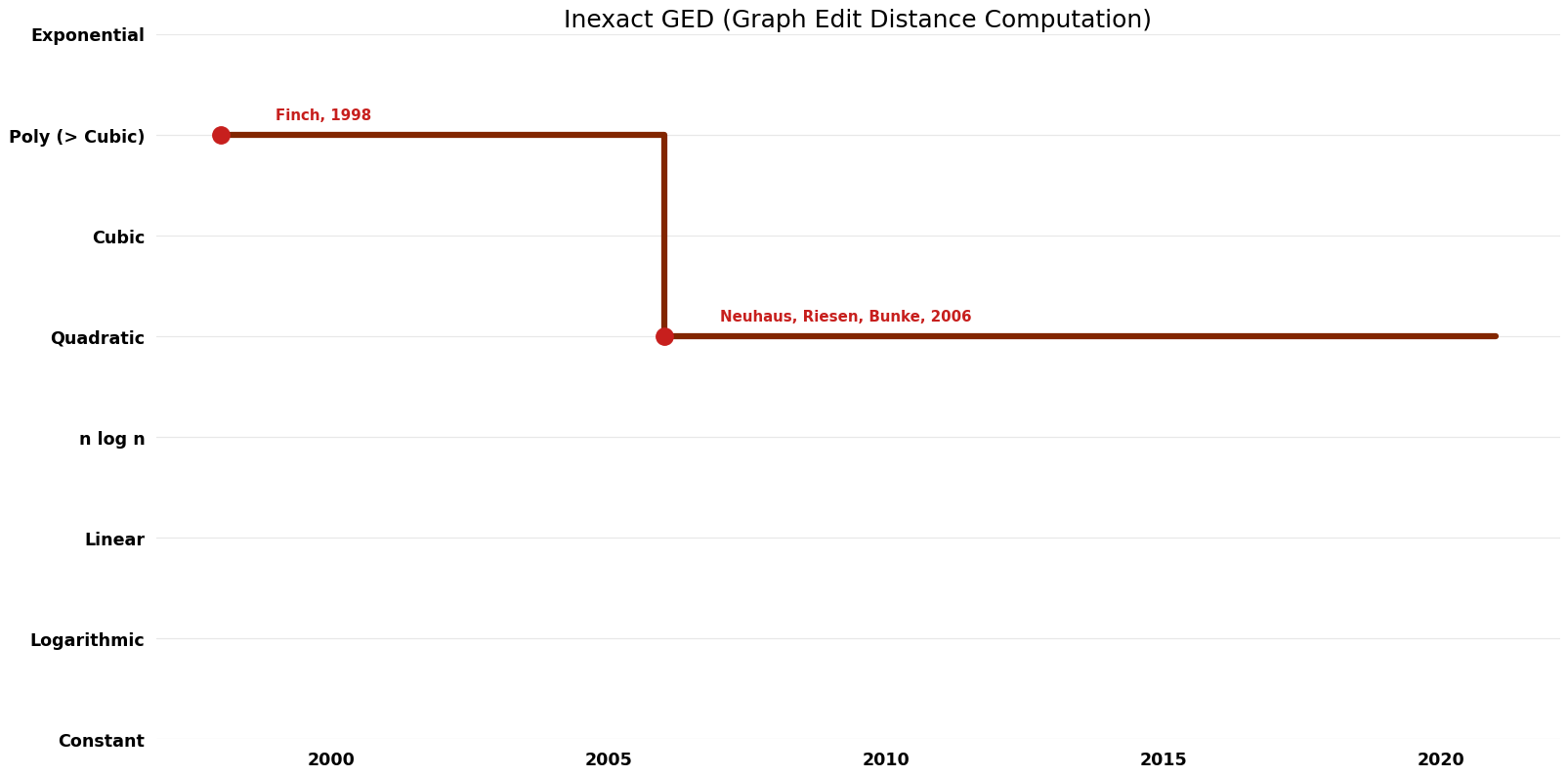
| Neuhaus, Riesen, Bunke | 2006 | $O(V^{2})$ | $O(wV)$ | Exact | Deterministic | Time |
| Wang Y-K; Fan K-C; Horng J-T | 1997 | $O(V E^{2} loglogE)$ | Exact | Deterministic | Time | |
| Tao D; Tang X; Li X et al | 2006 | $O(V^{2})$ | Exact | Deterministic | Time | |
| Finch | 1998 | $O(V^{2} E)$ | $O(V^{2})$? | Exact | Deterministic | Time |
Time Complexity Graph
Space Complexity Graph
Space-Time Tradeoff Improvements
