3-Graph Coloring (Graph Coloring)

Description

In this case, we wish to determine whether or not a graph is 3-colorable.

Related Problems

Generalizations: k-Graph Coloring

Related: Chromatic Number, 2-Graph Coloring, 4-Graph Coloring, 5-Graph Coloring, #k-Graph Coloring, #2-Graph Coloring, #3-Graph Coloring, #4-Graph Coloring, #5-Graph Coloring

Parameters

n: number of vertices

m: number of edges

Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
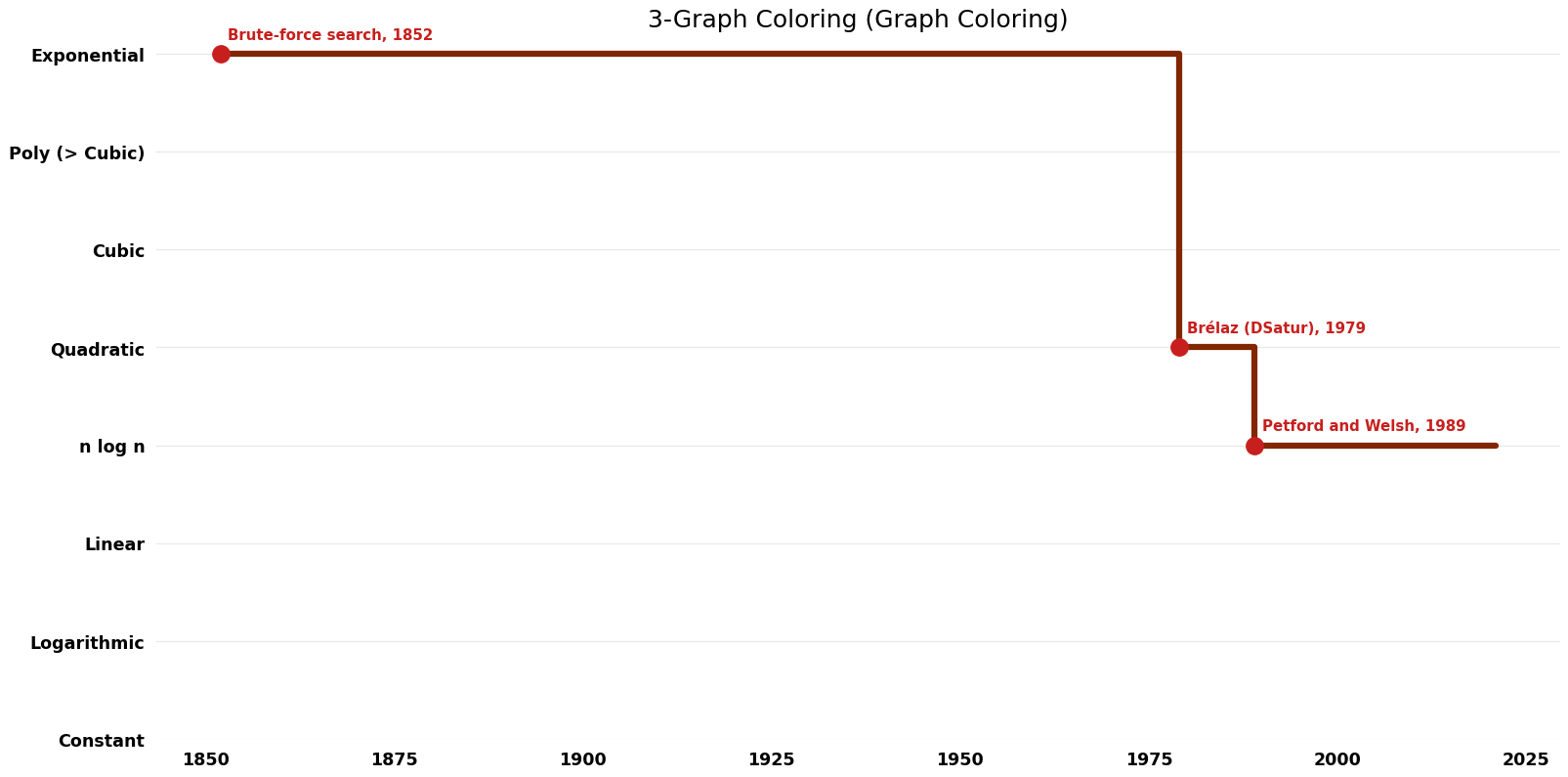
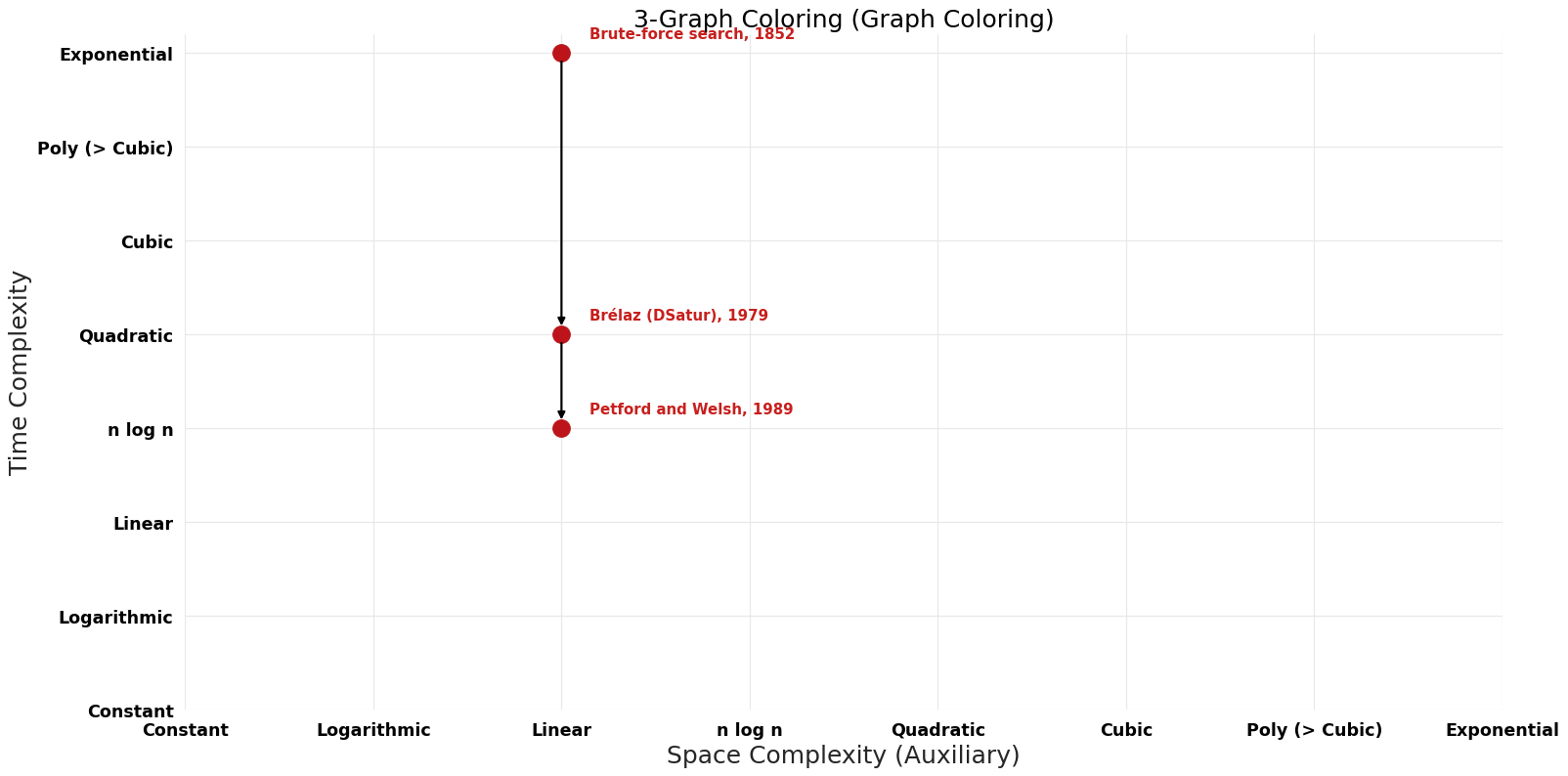
Brute-force search	1852	$O((n+m)*{3}^n)$	$O(n)$ auxiliary	Exact	Deterministic
Karger, Blum	1997	$O(poly(V))$		$\tilde{O}(n^{3/14})$	Deterministic	Time
Brélaz (DSatur)	1979	$O(V^{2})$	$O(V + E)$	Exact	Deterministic	Time
Petford and Welsh	1989	$O(nlogn)$	$O(n)$	Exact	Randomized	Time
Lawler	1976	$O(m*n*{3}^{(n/{3})}) ~ O(mn({1.445})^n)$	$O(n+m)$	Exact	Deterministic	Time
Schiermeyer	1994	$O({1.415}^n)$	$O(nm+n^{2})$ loose bound, possibly $O(n+m)$?	Exact	Deterministic	Time
Beigel & Eppstein	1995	$O({1.3446}^n)$	$O(n^{2})$?	Exact	Deterministic	Time
Beigel & Eppstein	2000	$O({1.3289}^n)$	$O(n^{2})$?	Exact	Deterministic	Time
Robson	1986	$O({1.2108}^n)$		Exact	Deterministic	Time
Schöning	1999	$O({1.333}^n)$		Exact	Randomized	Time
Hirsch	1998	$O({1.239}^n)$		Exact	Deterministic	Time
Johnson	1988	$O({1.4422}^n)$		Exact	Deterministic	Time
Alon and Kahale	1997	$O({1.24}^n)$		Exact	Deterministic	Time

Time Complexity graph

Space Complexity graph

Pareto Decades graph

References/Citation

https://www.sciencedirect.com/science/article/pii/S0196677404001117?via%3Dihub