CFG Parsing (CFG Problems)

Description

Given a grammar $G$ and a string $s$, find the parse structure, or analysis, assigned to the string $s$ by the grammar $G$.

Related Problems

Related: CFG Recognition

Parameters

n: length of the given string

Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
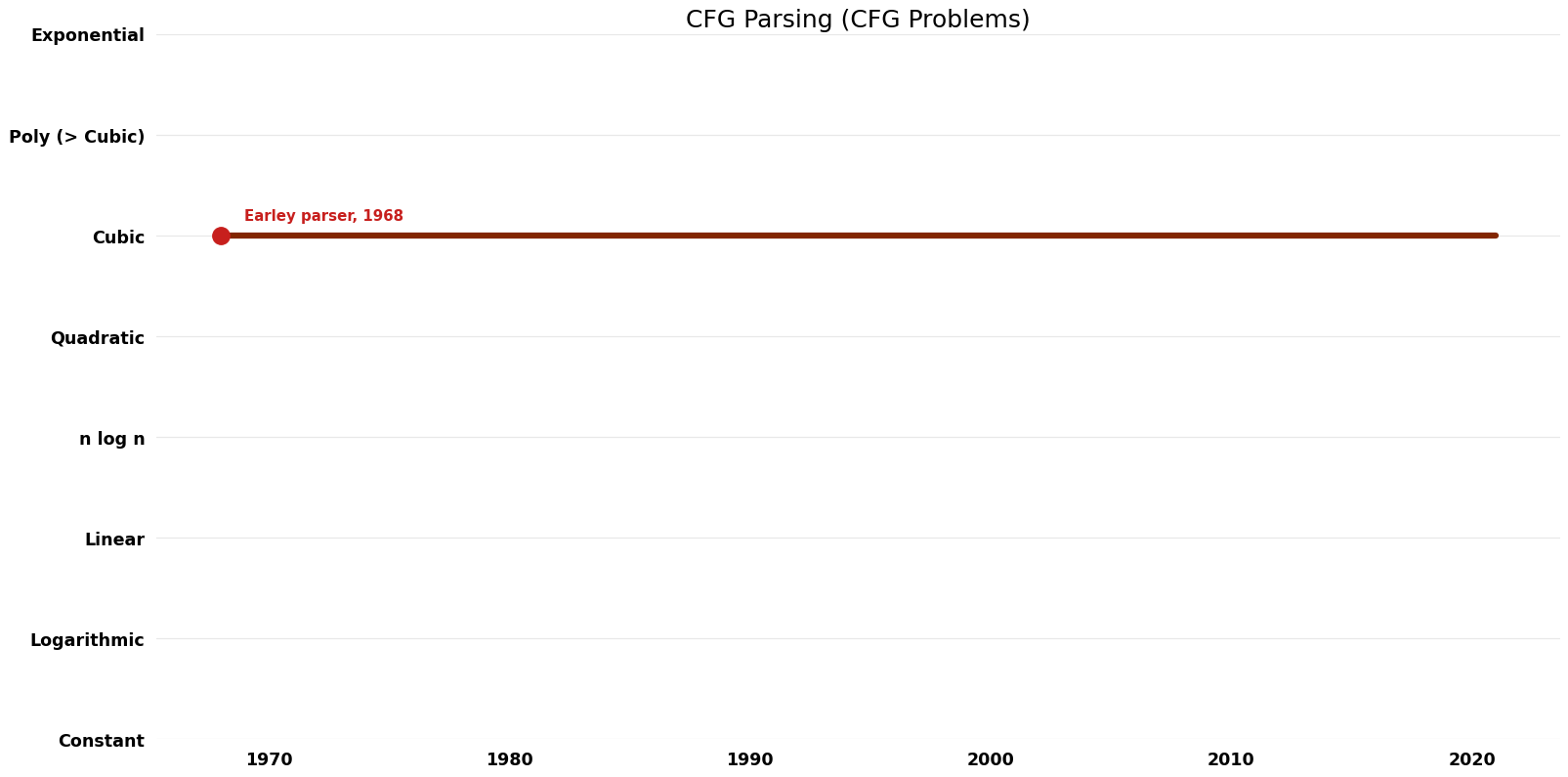
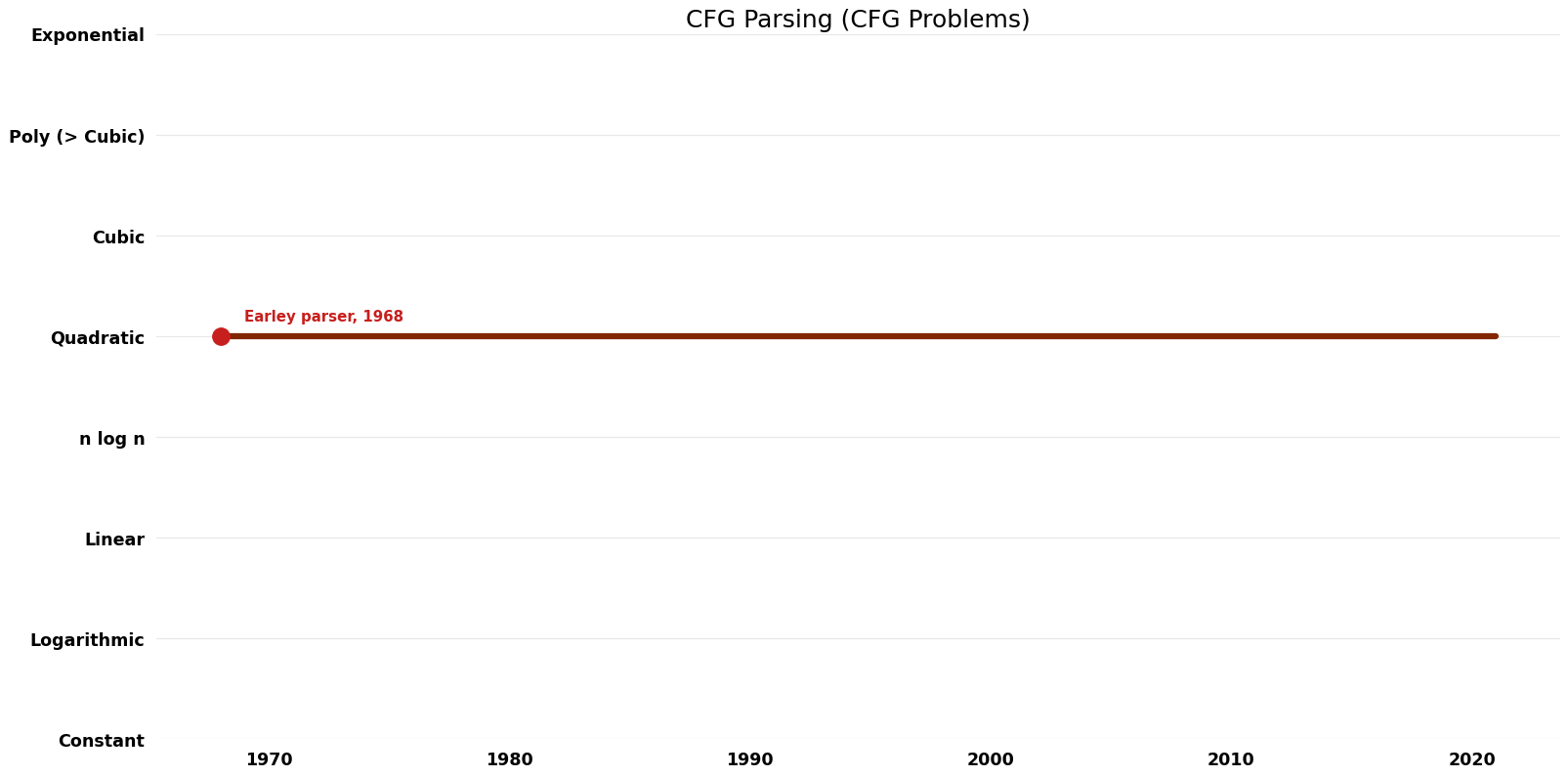
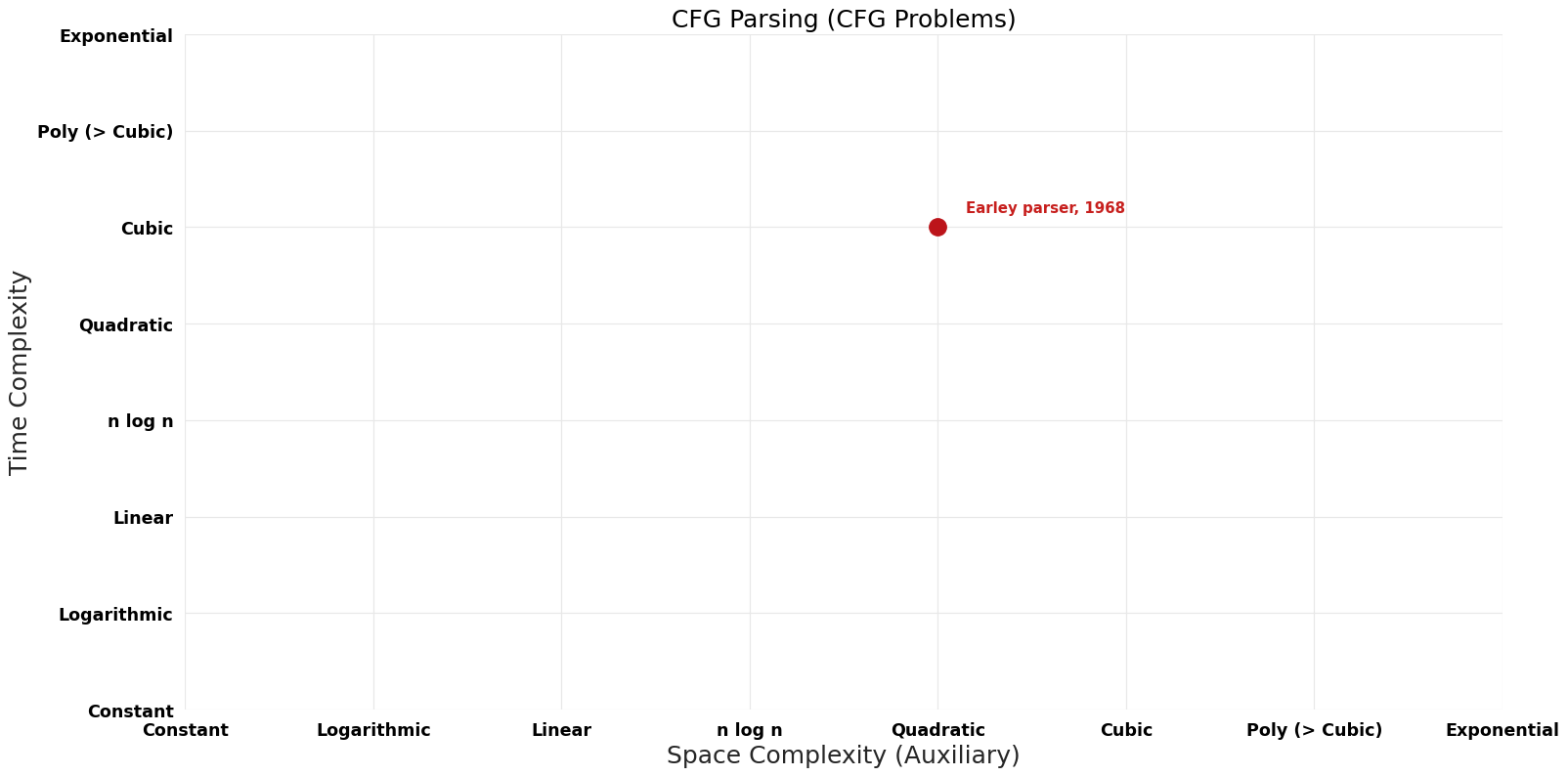
Earley parser	1968	$O(n^{3})$	$O(n^{2})$	Exact	Deterministic	Time & Space
GLR parser	1974	$O(n^{3})$	$O(n^{3})$	Exact	Deterministic	Time & Space

Time Complexity graph

Space Complexity graph

Pareto Decades graph

Reductions TO Problem

Problem	Implication	Year	Citation	Reduction
BMM	if: to-time: $O(n^{3-\epsilon})$ for some $\epsilon > {0}$ where $n \times n$ matrix then: from-time: $O(gn^{3-\epsilon})$ where $g$ is the size of the CFG	1975	https://www.sciencedirect.com/science/article/pii/S0022000075800468	link

Reductions FROM Problem

Problem	Implication	Year	Citation	Reduction
BMM	if: to-time: $O(gn^{3-\epsilon})$ for some $\epsilon > {0}$ where $g$ is the size of the CFG and $n$ is the size of the string then: from-time: $O(n^{3-\epsilon/3})$ where $n \times n$ matrix	2002	https://arxiv.org/abs/cs/0112018	link

References/Citation

https://link.springer.com/chapter/10.1007%2F978-3-662-21545-6_18