Square Matrix LU Decomposition (LU Decomposition)
Revision as of 10:20, 15 February 2023 by Admin (talk | contribs) (Created page with "{{DISPLAYTITLE:Square Matrix LU Decomposition (LU Decomposition)}} == Description == Lower–upper (LU) decomposition or factorization factors a matrix as the product of a lower triangular matrix and an upper triangular matrix. In this specific case, the input is a square $n \times n$ matrix == Related Problems == Generalizations: Rectangular Matrix LU Decomposition == Parameters == <pre>$n$: dimension of square matrix</pre> == Table of Algorithms == {| cl...")
Description
Lower–upper (LU) decomposition or factorization factors a matrix as the product of a lower triangular matrix and an upper triangular matrix. In this specific case, the input is a square $n \times n$ matrix
Related Problems
Generalizations: Rectangular Matrix LU Decomposition
Parameters
$n$: dimension of square matrix
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
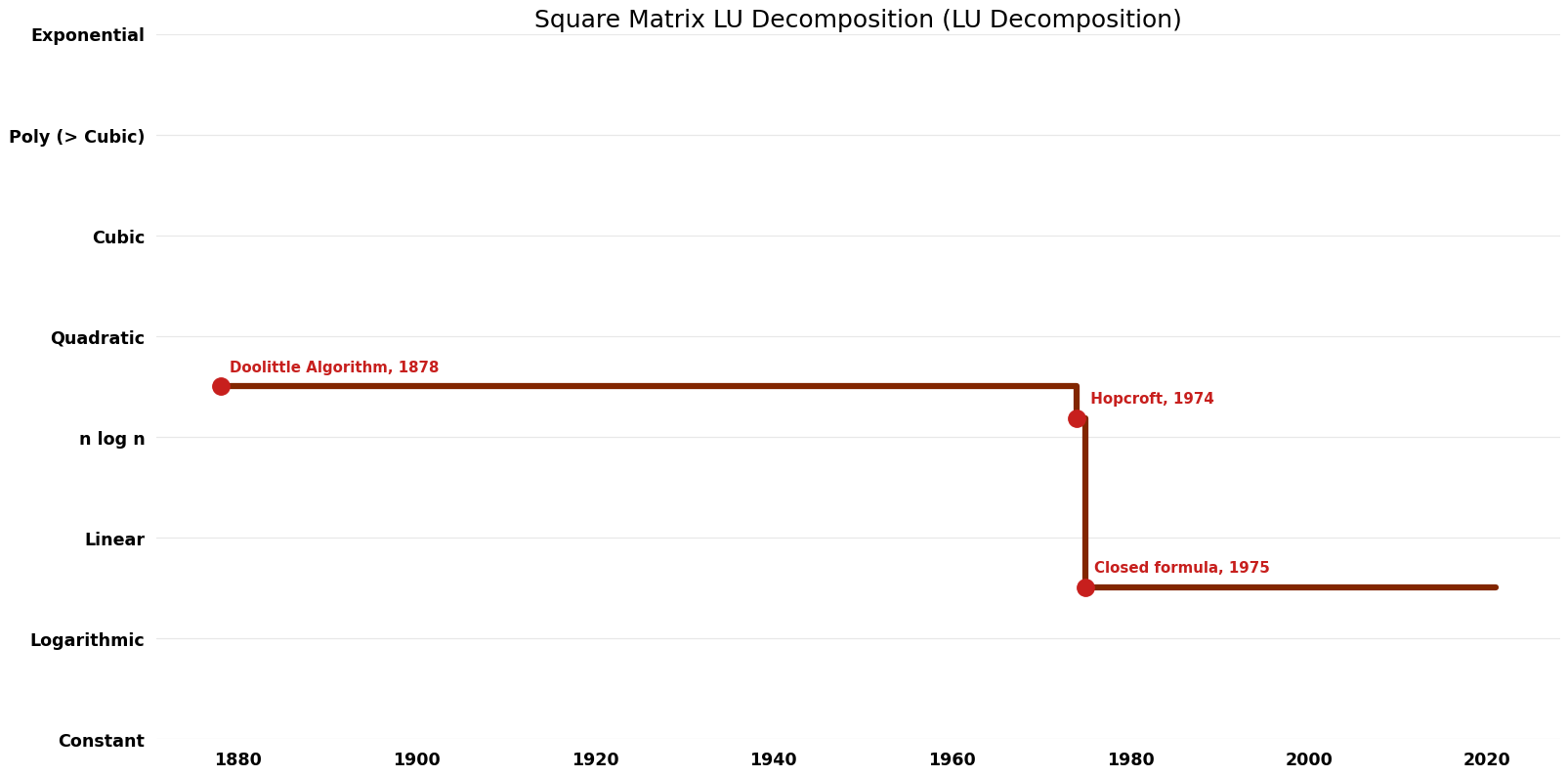
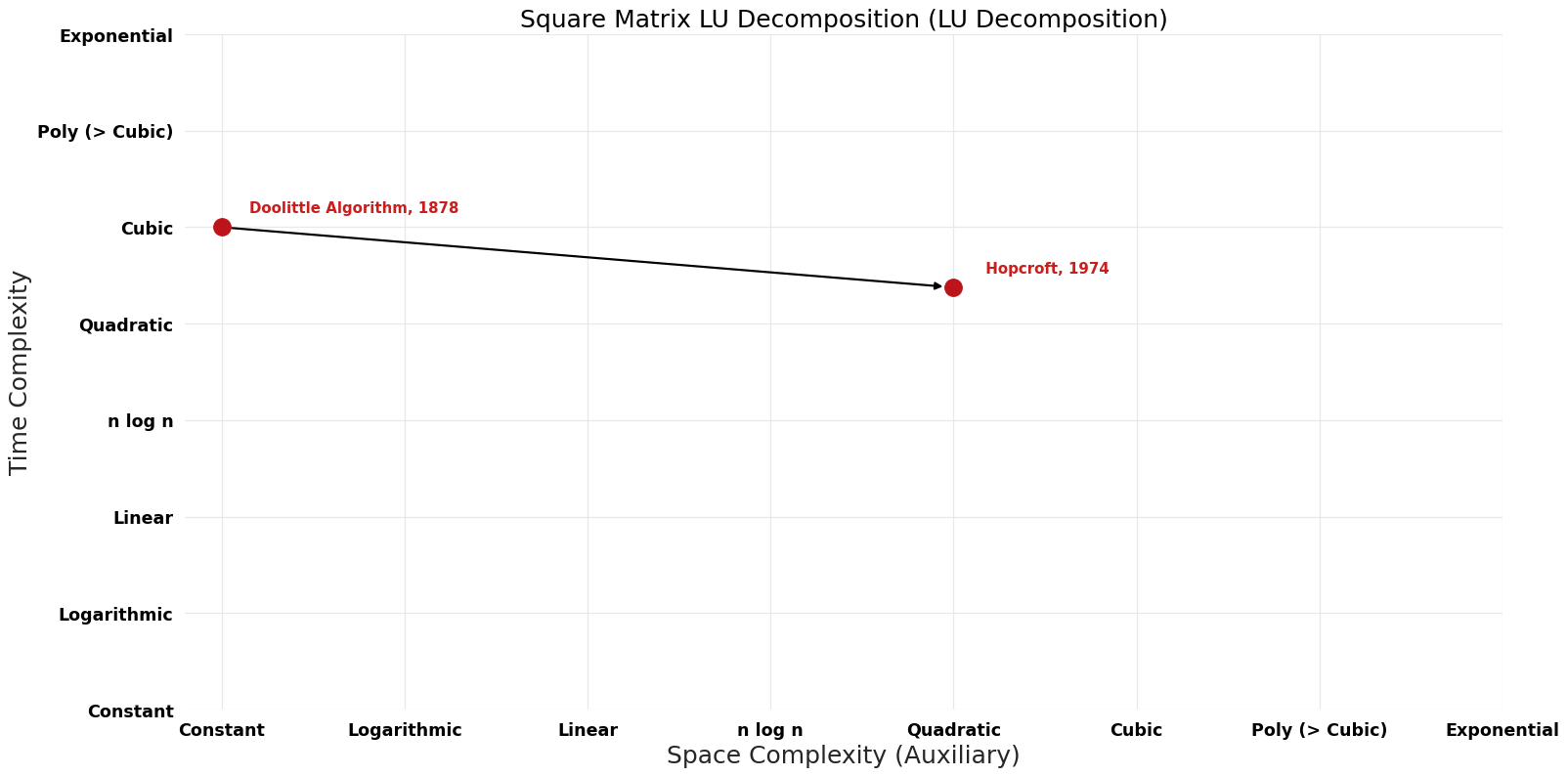
| Doolittle Algorithm | 1878 | $O(n^{3})$ | $\tilde{O}({1})$ | Exact | Deterministic | |
| Crout and LUP algorithms | 2007 | $O(n^{3})$ | $\tilde{O}({1})$ | Exact | Deterministic | Time |
| Okunev; Johnson | 1997 | $O(n^{3})$ | $O({1})$ | Exact | Deterministic | Time |
| Bunch; Hopcroft | 1974 | $O(n^{2.{37}6})$ | $\tilde{O}(n^{2})$ | Exact | Deterministic | Time |
| Closed formula | 1975 | $O(nlogn)$ | Exact | Deterministic | ||
| David | 2006 | $O(nlogn)$ | Exact | Deterministic | ||
| Press, Teukolsky, Flannery | 2007 | $O(n^{3})$ | $\tilde{O}(n)$ | Exact | Deterministic | Time |
Time Complexity graph
Space Complexity graph
Pareto Decades graph
