kth Order Statistic (kth Order Statistic)
Revision as of 11:17, 15 February 2023 by Admin (talk | contribs) (Created page with "{{DISPLAYTITLE:kth Order Statistic (kth Order Statistic)}} == Description == An algorithm seeks to find the $k^{th}$ order statistic of a statistical sample, or the $k^{th}$-smallest value in a list or array. == Parameters == <pre>n: size of list</pre> == Table of Algorithms == {| class="wikitable sortable" style="text-align:center;" width="100%" ! Name !! Year !! Time !! Space !! Approximation Factor !! Model !! Reference |- | Naive Selection (kth Order St...")
Description
An algorithm seeks to find the $k^{th}$ order statistic of a statistical sample, or the $k^{th}$-smallest value in a list or array.
Parameters
n: size of list
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
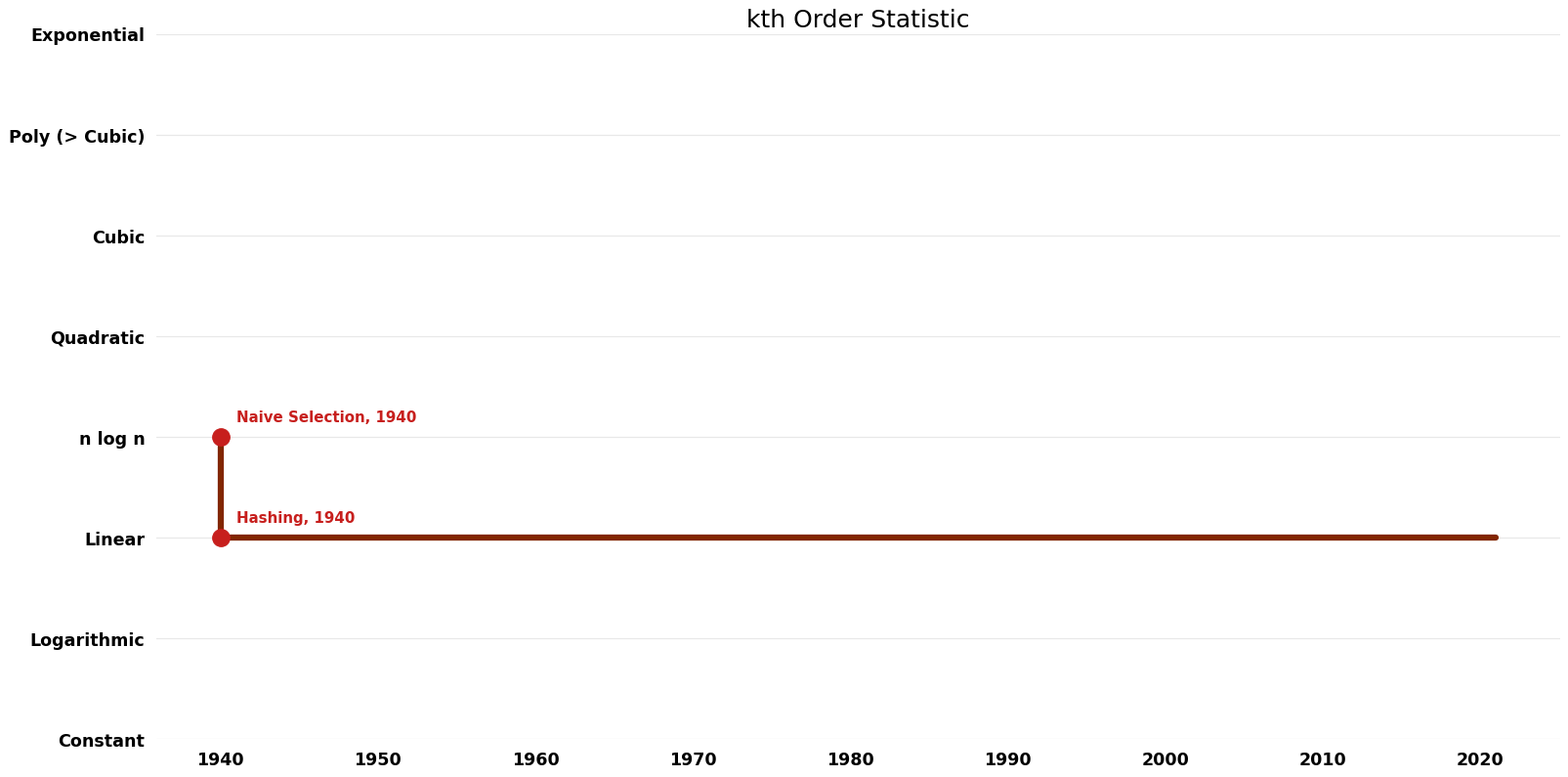
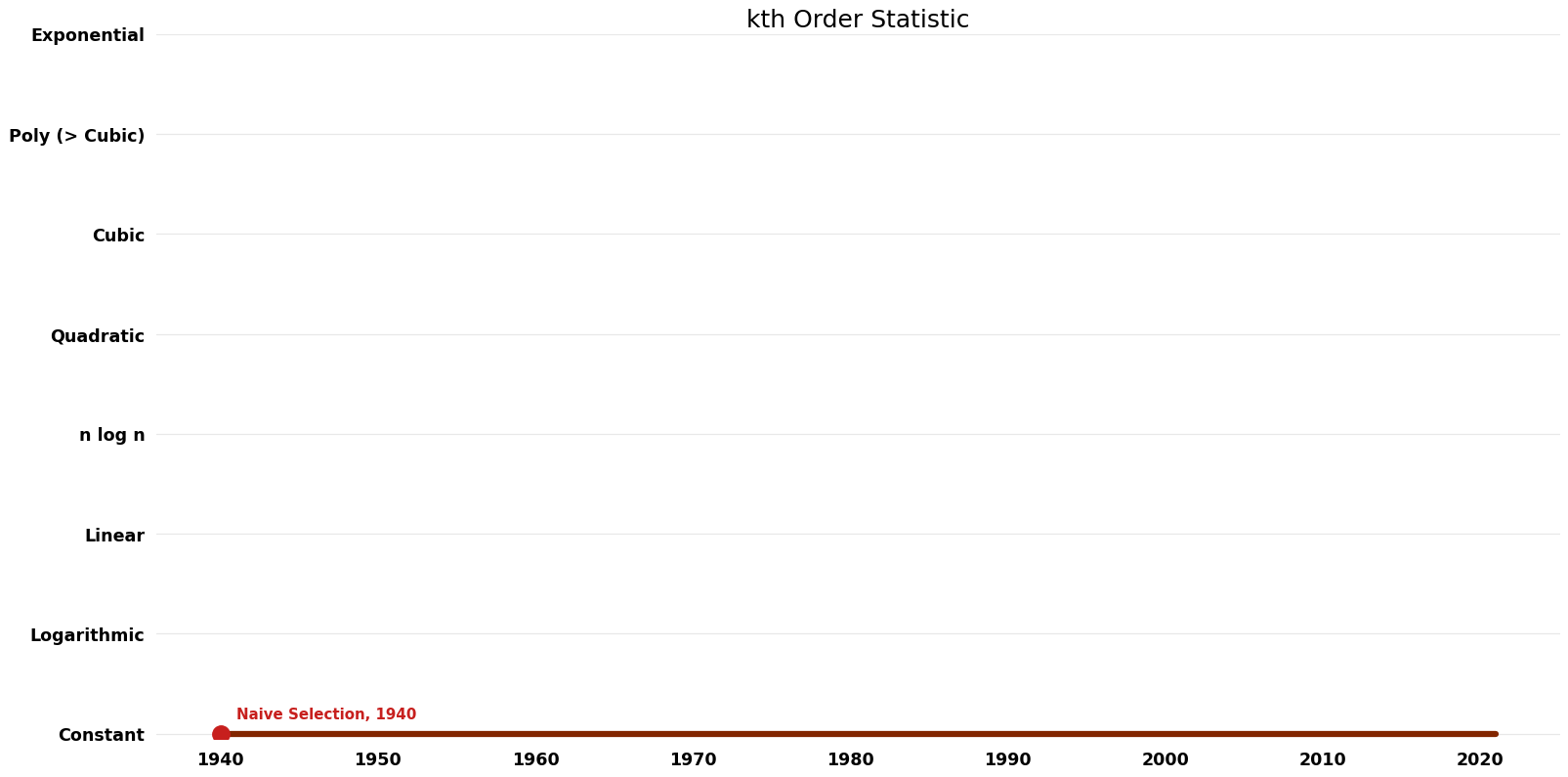
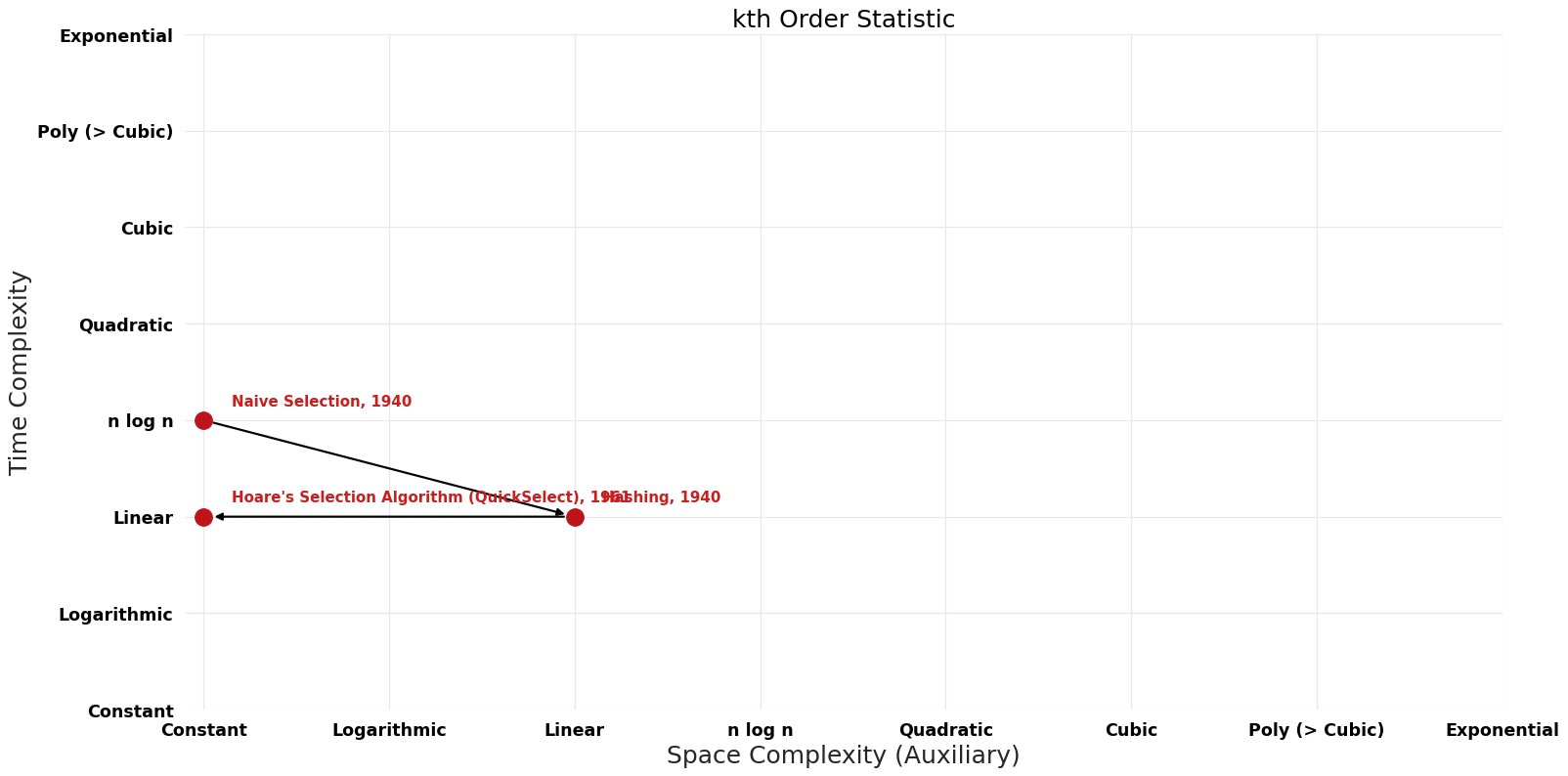
| Naive Selection | 1940 | $O(nlogn)$ | $O({1})$ (can use in-situ sorting) | Exact | Deterministic | |
| Hoare's Selection Algorithm (QuickSelect) | 1961 | $O(n)$ | $O({1})$ (in-situ) | Exact | Deterministic | Time |
| Hashing | 1940 | $O(n)$ | $O(n)$ | Exact | Deterministic |
Time Complexity graph
Space Complexity graph
Pareto Decades graph
References/Citation
https://11011110.github.io/blog/2007/10/09/blum-style-analysis-of.html