Convex Hull
Revision as of 11:54, 10 October 2022 by Admin (talk | contribs) (Created page with "== Problem Description== The Convex Hull is the line completely enclosing a set of points in a plane so that there are no concavities in the line. More formally, we can describe it as the smallest convex polygon which encloses a set of points such that each point in the set lies within the polygon or on its perimeter. == Bounds Chart == 1050px == Step Chart == 1050px == Improvement Table == {| class...")
Problem Description
The Convex Hull is the line completely enclosing a set of points in a plane so that there are no concavities in the line. More formally, we can describe it as the smallest convex polygon which encloses a set of points such that each point in the set lies within the polygon or on its perimeter.
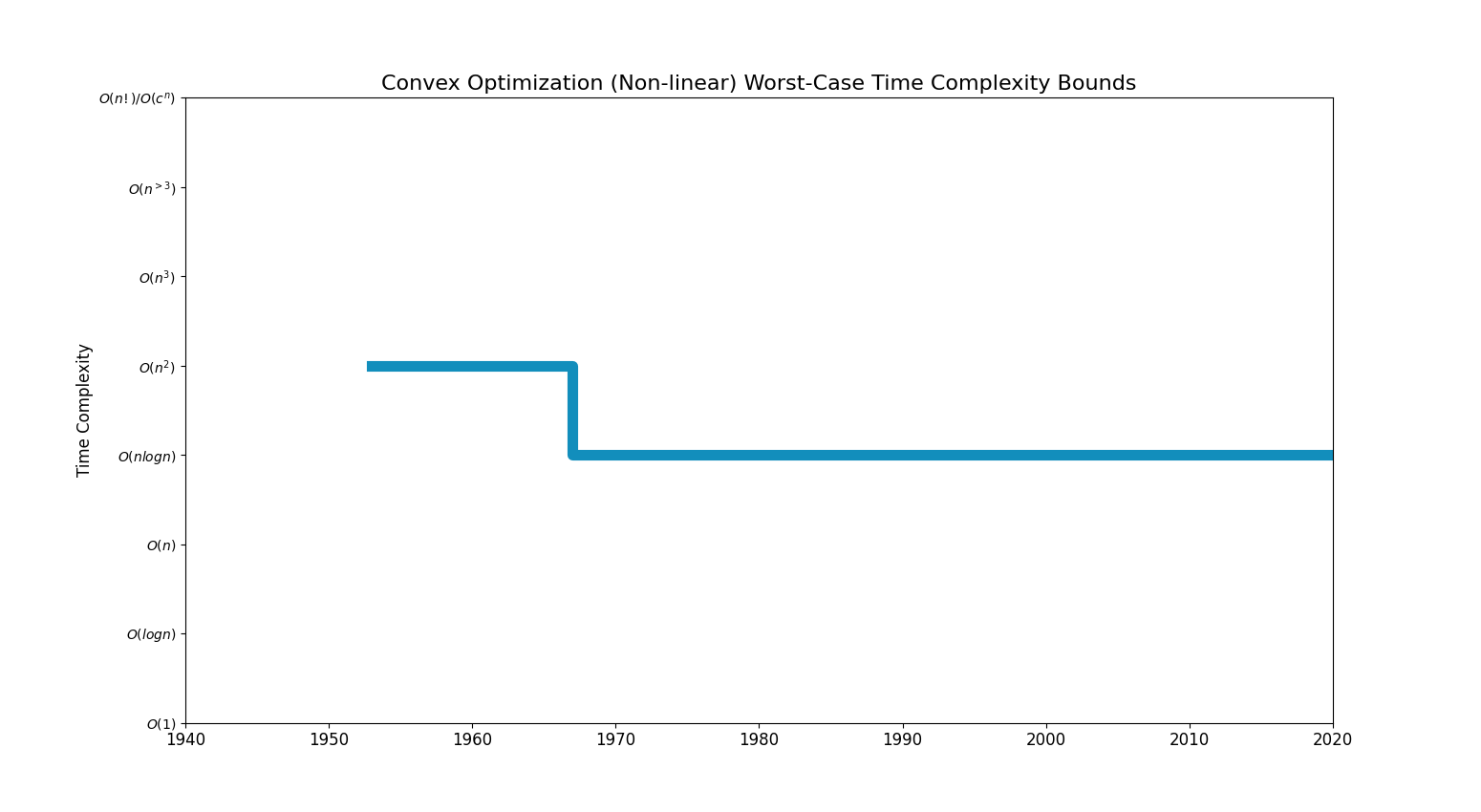
Bounds Chart
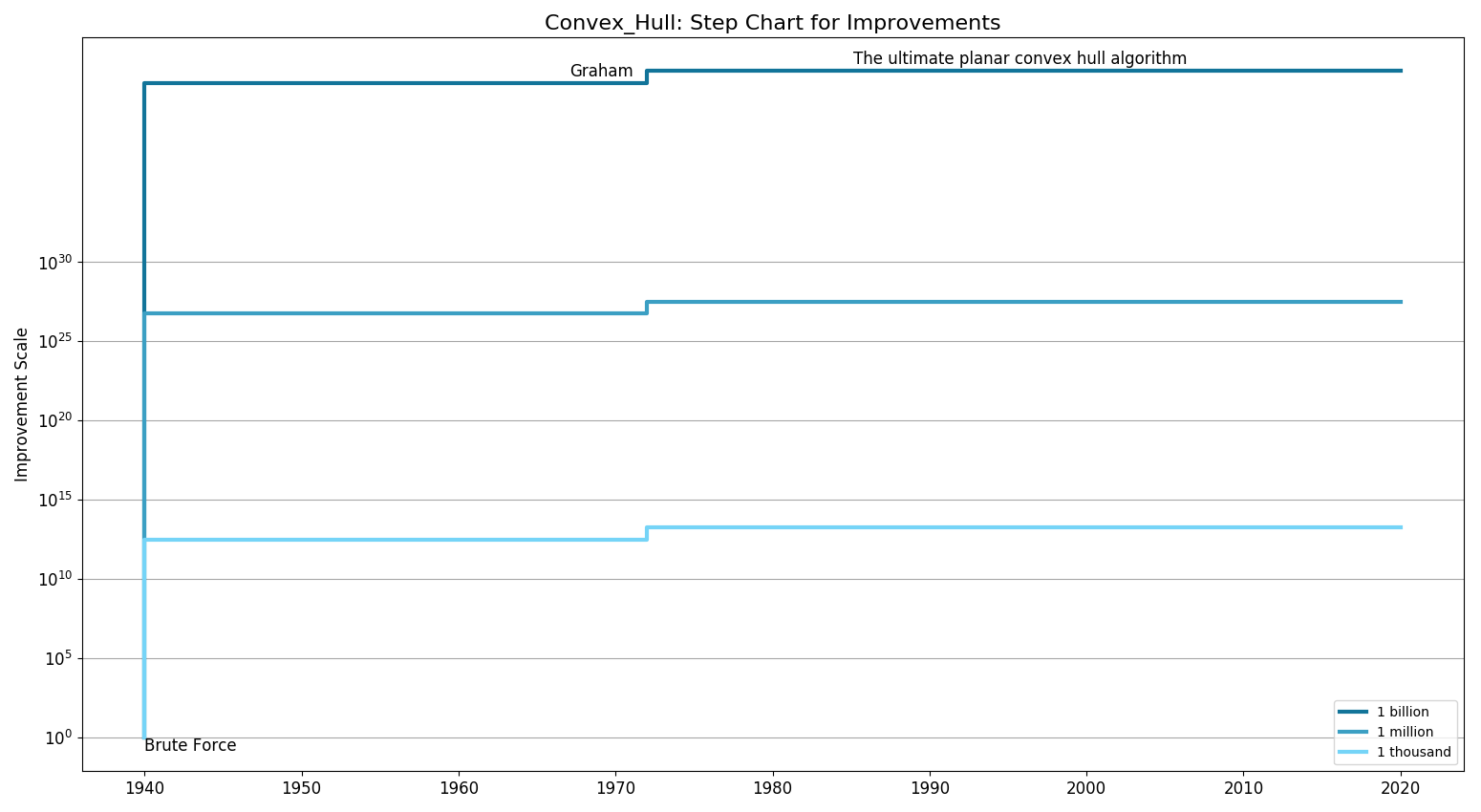
Step Chart
Improvement Table
| Complexity Classes | Algorithm Paper Links | Lower Bounds Paper Links |
|---|---|---|
| Exp/Factorial | ||
| Polynomial > 3 | ||
| Cubic | [Brute Force (1935)] | |
| Quadratic | ||
| nlogn | Graham (1972)
W. Eddy Quickhull; 1977 (1977) Incremental convex hull algorithm; Michael Kallay (1984) |
|
| Linear | ||
| logn | Miller; Stout 1988 (1988) |