Topological Sorting
Revision as of 12:01, 10 October 2022 by Admin (talk | contribs) (Created page with "== Problem Description== Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge u v, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG. Topological Sorting is mainly used for scheduling jobs from the given dependencies among jobs. In computer science, applications of this type arise in instruction scheduling, ordering of formula cell evaluati...")
Problem Description
Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge u v, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.
Topological Sorting is mainly used for scheduling jobs from the given dependencies among jobs. In computer science, applications of this type arise in instruction scheduling, ordering of formula cell evaluation when recomputing formula values in spreadsheets, logic synthesis, determining the order of compilation tasks to perform in make files, data serialization, and resolving symbol dependencies in linkers.
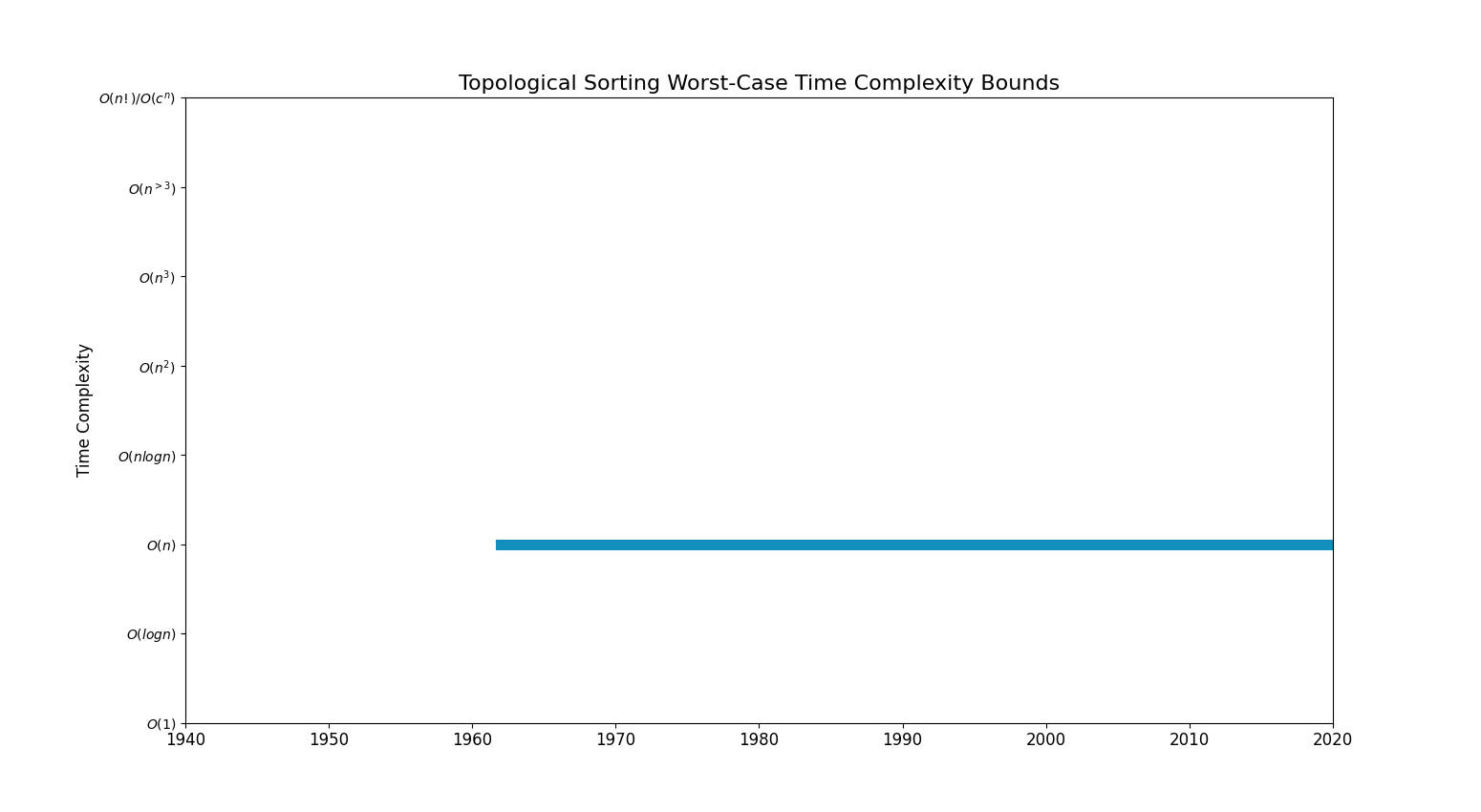
Bounds Chart
Step Chart
Improvement Table
| Complexity Classes | Algorithm Paper Links | Lower Bounds Paper Links |
|---|---|---|
| Exp/Factorial | ||
| Polynomial > 3 | ||
| Cubic | ||
| Quadratic | ||
| nlogn | ||
| Linear | Kahn's algorithm (1962) | |
| logn | Dekel; Nassimi & Sahni (1981) Parallel Implementation (1981) |