Min. Spanning Tree
Problem Description
The cost of the spanning tree is the sum of the weights of all the edges in the tree. There can be many spanning trees. Minimum spanning tree is the spanning tree where the cost is minimum among all the spanning trees. There also can be many minimum spanning trees.
Minimum spanning tree has direct application in the design of networks. It is used in algorithms approximating the travelling salesman problem, multi-terminal minimum cut problem and minimum-cost weighted perfect matching. Other practical applications are:
Cluster Analysis
Handwriting recognition
Image segmentation
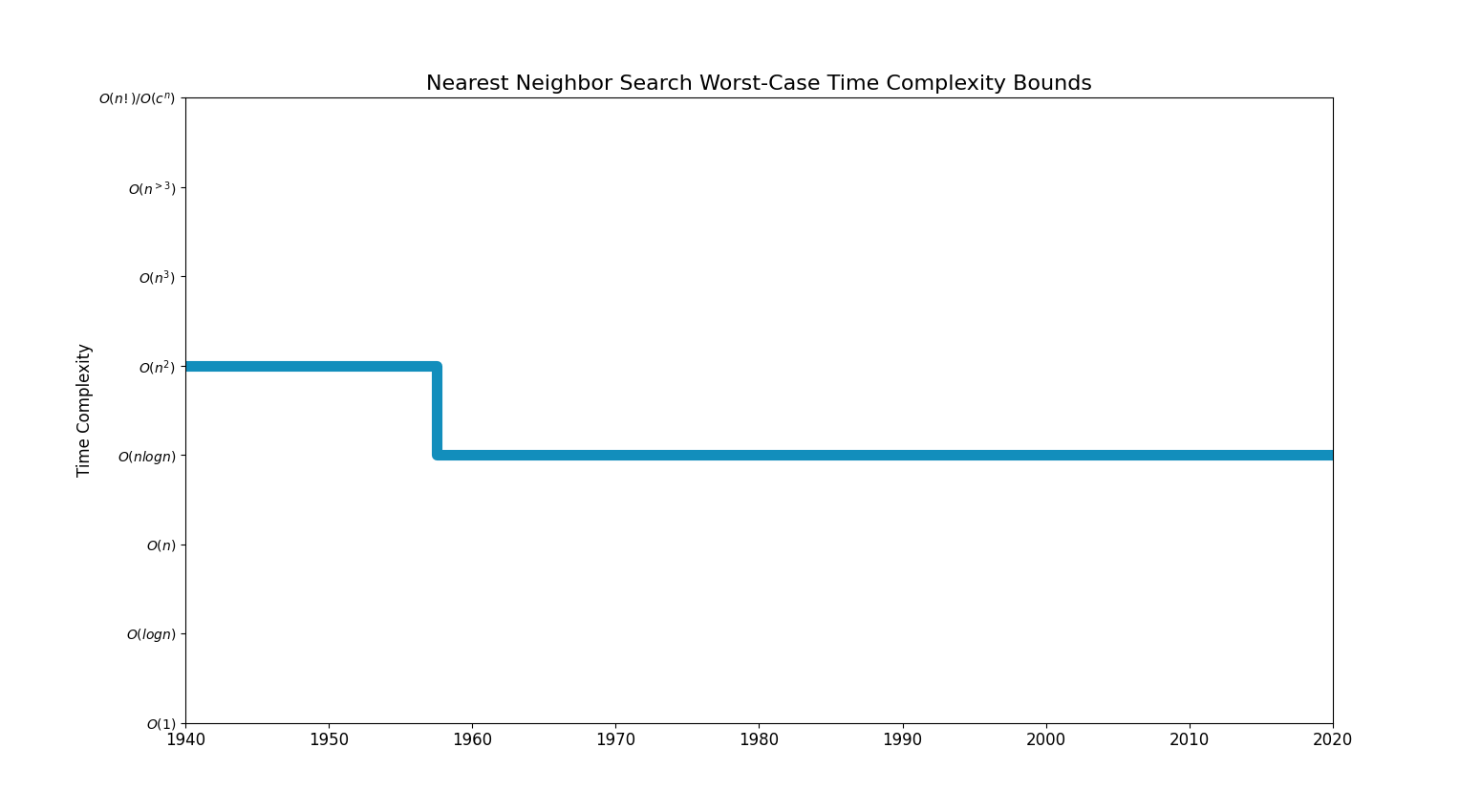
Bounds Chart
Step Chart
Improvement Table
| Complexity Classes | Algorithm Paper Links | Lower Bounds Paper Links |
|---|---|---|
| Exp/Factorial | ||
| Polynomial > 3 | ||
| Cubic | ||
| Quadratic | Thorup 2000 (2000)
Quick Kruskal algorithm (2006) Kruskal’s algorithm with demand-sorting (1991) Prim's algorithm + Fibonacci heaps; Fredman & Tarjan (1957) Hong’s algorithm (2013) CH Algorithm (2004) OBF Algorithm (2011) |
|
| nlogn | Fliter Kruskal algorithm (2009)
Cheriton-Tarjan Algorithm (1976) Yao's algorithm (1975) Kruskal's algorithm (1956) Prim's algorithm + Fibonacci heaps; Fredman & Tarjan (1987) Munro’s algorithm (1971) [- Borůvka's algorithm (1926)] |
|
| Linear | Karger; Klein & Tarjan (1995) (1995) | |
| logn | Bader & Cong (2006) Parallel Implementation (2006) |