Matrix Multiplication
Revision as of 11:58, 10 October 2022 by Admin (talk | contribs) (Created page with "== Problem Description== Matrix multiplication or multiplication of matrices is one of the operations that can be performed on matrices in linear algebra. Multiplication of matrix A with matrix B is possible when both the given matrices, A and B are compatible. Matrix multiplication is a binary operation, that gives a matrix from two given matrices. Matrix multiplication was first introduced in 1812 by French mathematician Jacques Philippe Marie Binet, in order to repre...")
Problem Description
Matrix multiplication or multiplication of matrices is one of the operations that can be performed on matrices in linear algebra. Multiplication of matrix A with matrix B is possible when both the given matrices, A and B are compatible. Matrix multiplication is a binary operation, that gives a matrix from two given matrices.
Matrix multiplication was first introduced in 1812 by French mathematician Jacques Philippe Marie Binet, in order to represent linear maps using matrices. Let us understand the rule for multiplication of matrices and matrix multiplication formula in detail in the following sections.
Bounds Chart
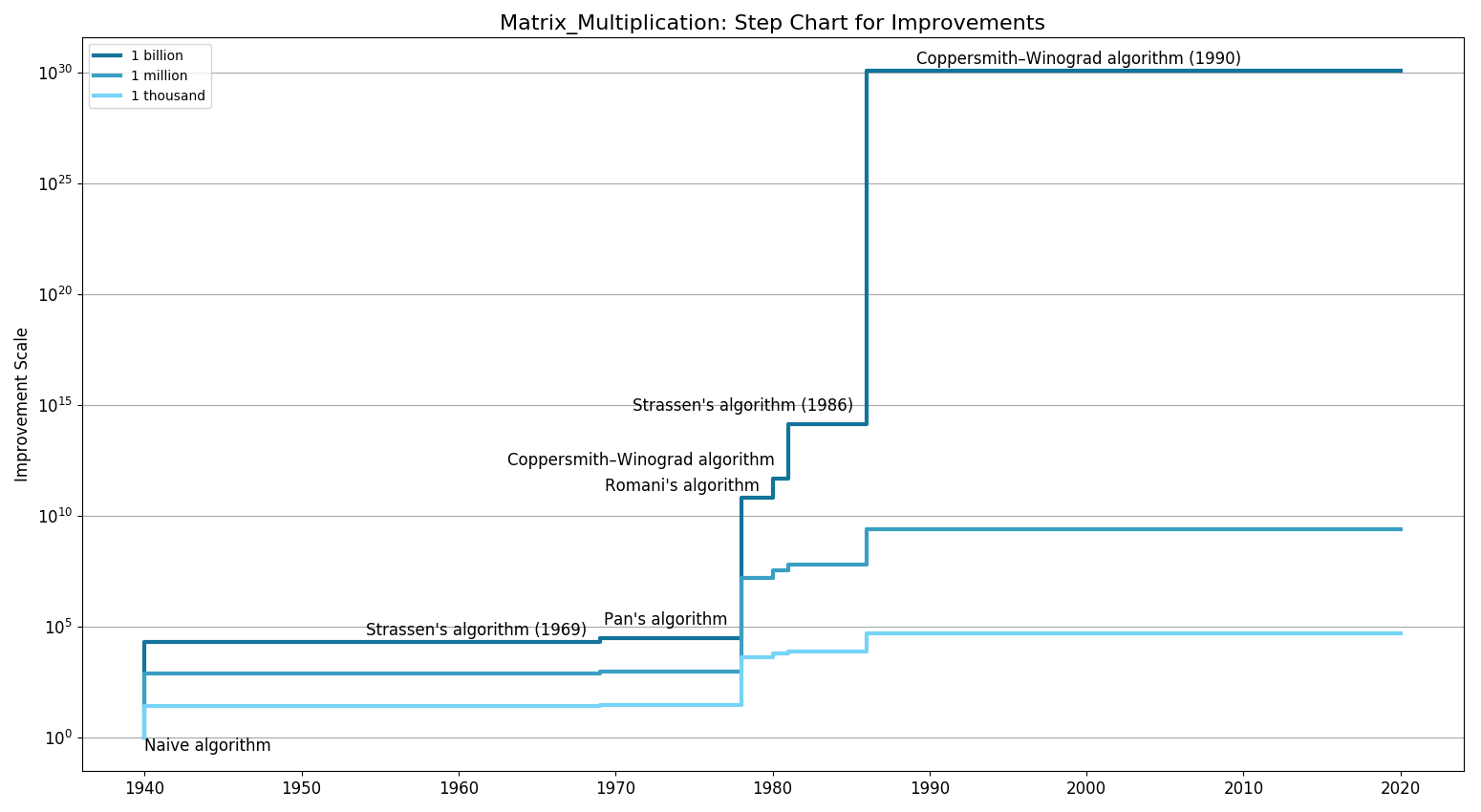
Step Chart
Improvement Table
| Complexity Classes | Algorithm Paper Links | Lower Bounds Paper Links |
|---|---|---|
| Exp/Factorial | ||
| Polynomial > 3 | ||
| Cubic | [- Naive algorithm (1940)]
Strassen's algorithm (1969) (1969) Coppersmith–Winograd algorithm (1981) [ Strassen's algorithm (1986) (1986)] |
|
| Quadratic | ||
| nlogn | ||
| Linear | ||
| logn |