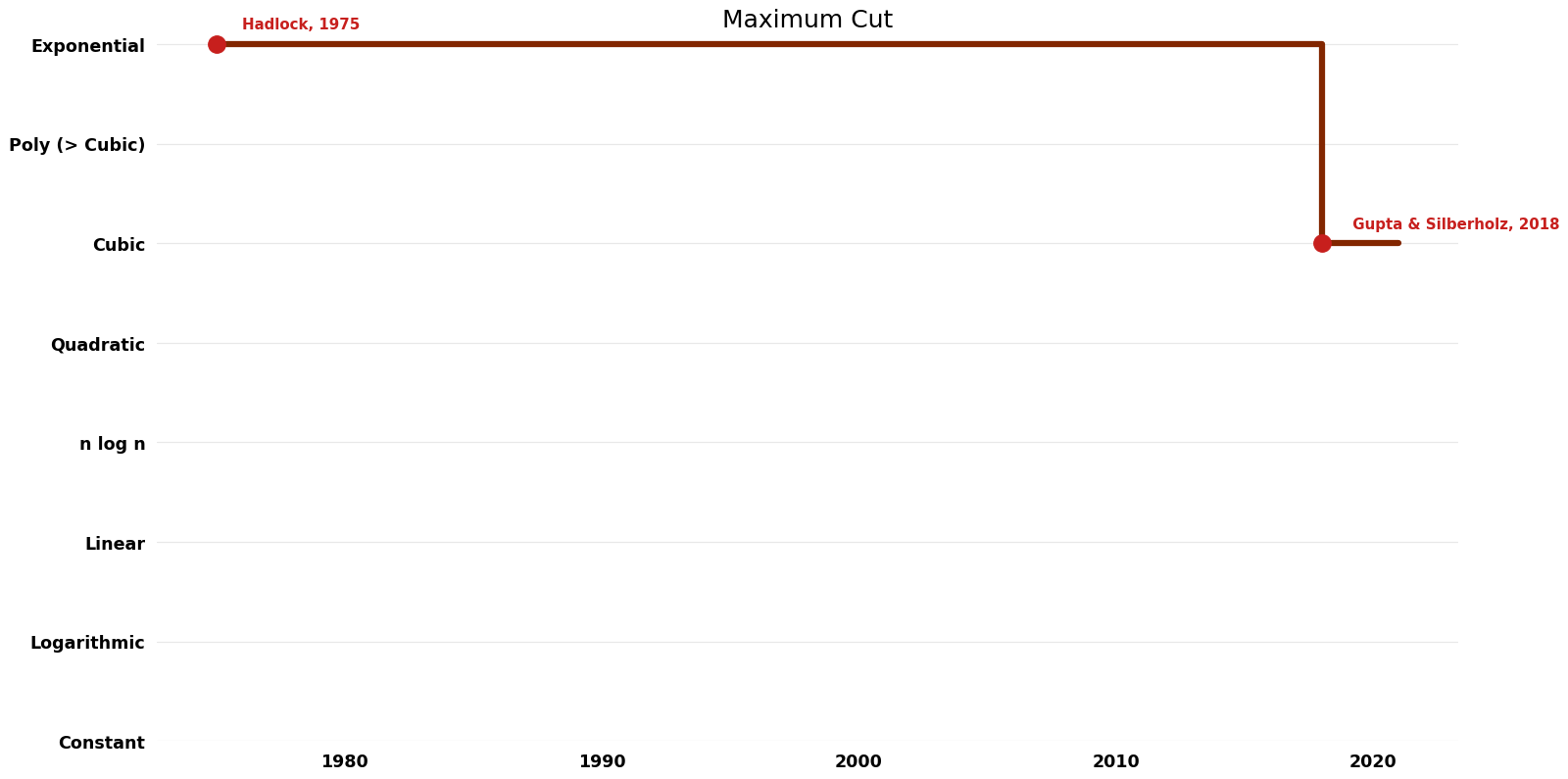
Maximum Cut (Maximum Cut)

Description

Given a graph $G=(V, E)$ with edge weights $c_e > 0$ for all $e\in E$, find a cut $\delta(W)$ such that $c(\delta(W)):=\Sigma_{e\in \dela(W)} c_e$ is as large as possible.

Parameters

n: number of vertices

m: number of edges

Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
Hadlock	1975	$O({2}^V)$		Exact	Deterministic
Motwani & Raghavan	1995	$O(V)$?	$O(V)$ auxiliary	0.5	Randomized	Time
Mitzenmacher & Upfal	2005	$O(VE)$?	$O(V)$ auxiliary	0.5	Deterministic	Time
Khuller; Raghavachari & Young, "Greedy Methods"	2007	$O(V^{2})$?	$O(V)$ auxiliary	0.5	Deterministic	Time
Ausiello et al.	2003	$O(V^{3} logE)$	$O(V^{2})$?	~0.878; assuming this is the goemans-williamson algorithm	Deterministic	Time
Dunning; Gupta & Silberholz	2018	$O(VE)$		Exact	Deterministic	Time

Time Complexity Graph