Digraph Realization Problem (Graph Realization Problems)
Jump to navigation
Jump to search
Description
Given a sequence $S := (a_1, b_1), \ldots, (a_n, b_n)$ with $a_i, b_i \in \mathbb{Z}_0^+$, does there exist a directed graph (no parallel arcs allowed) with labeled vertex set $V := \{v_1, \ldots , v_n\}$ such that for all $v_i \in V$ indegree and outdegree of $v_i$ match exactly the given numbers $a_i$ and $b_i$, respectively?
Related Problems
Subproblem: DAG Realization Problem
Parameters
$n$: number of degree pairs
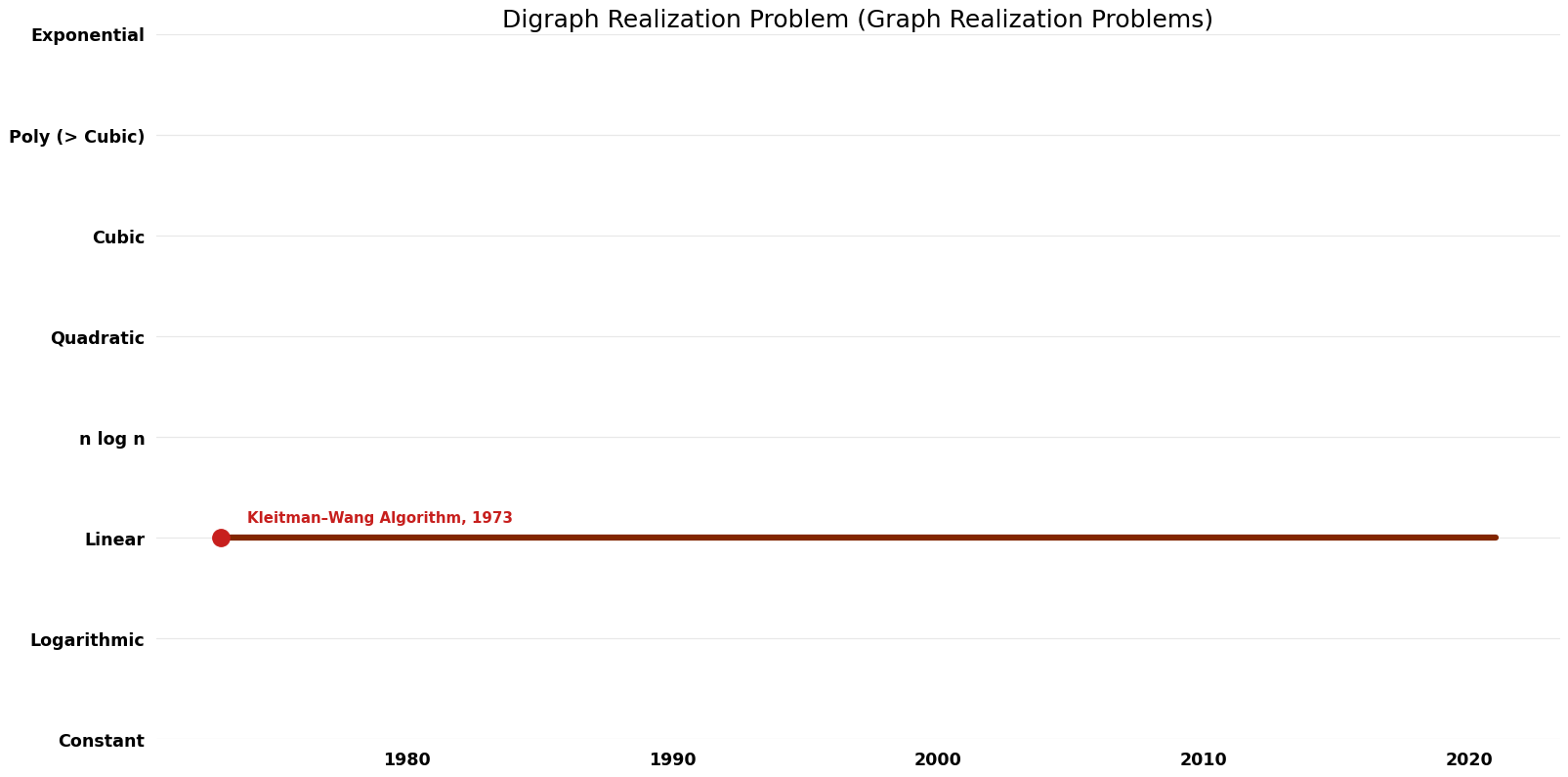
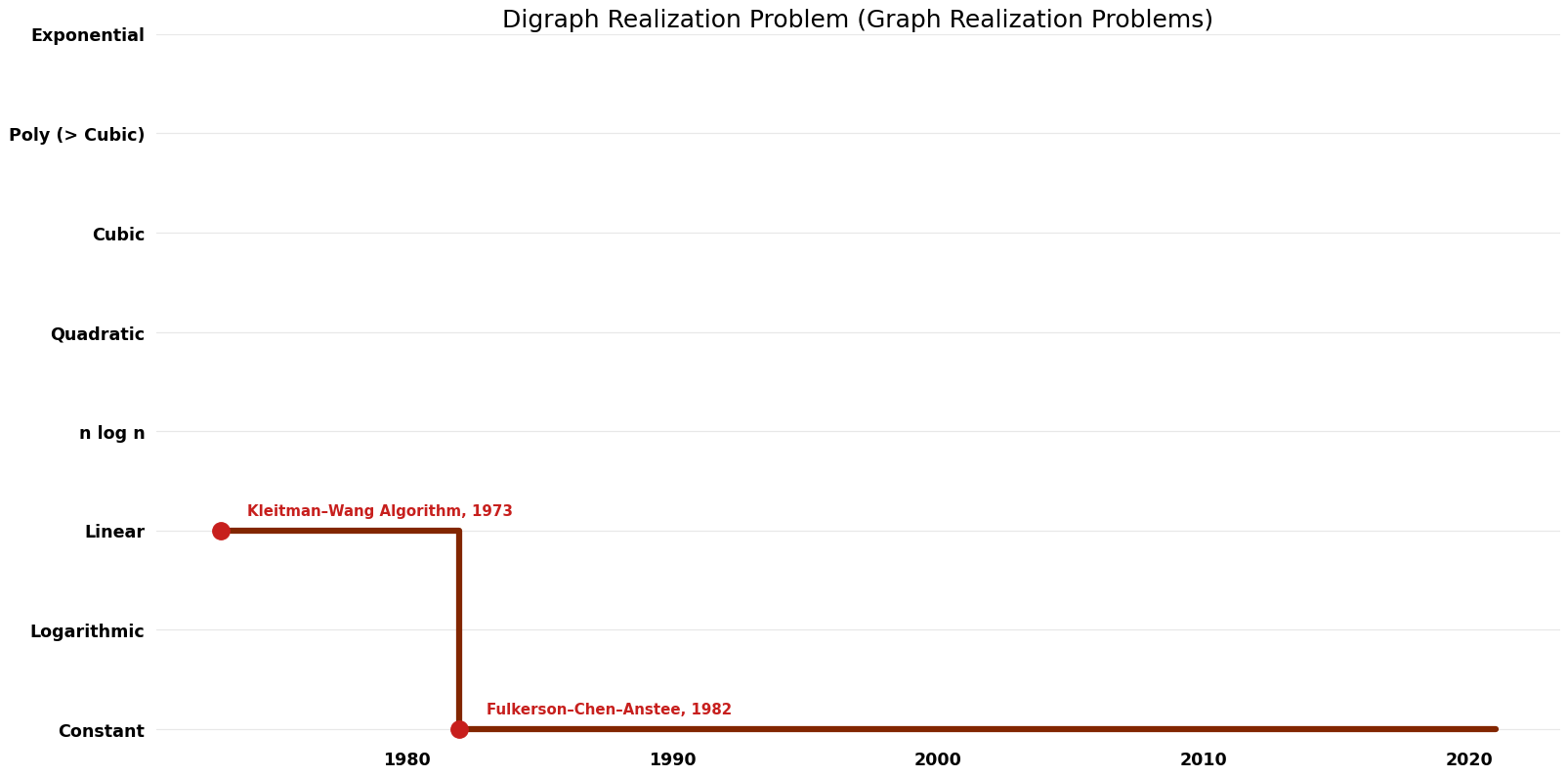
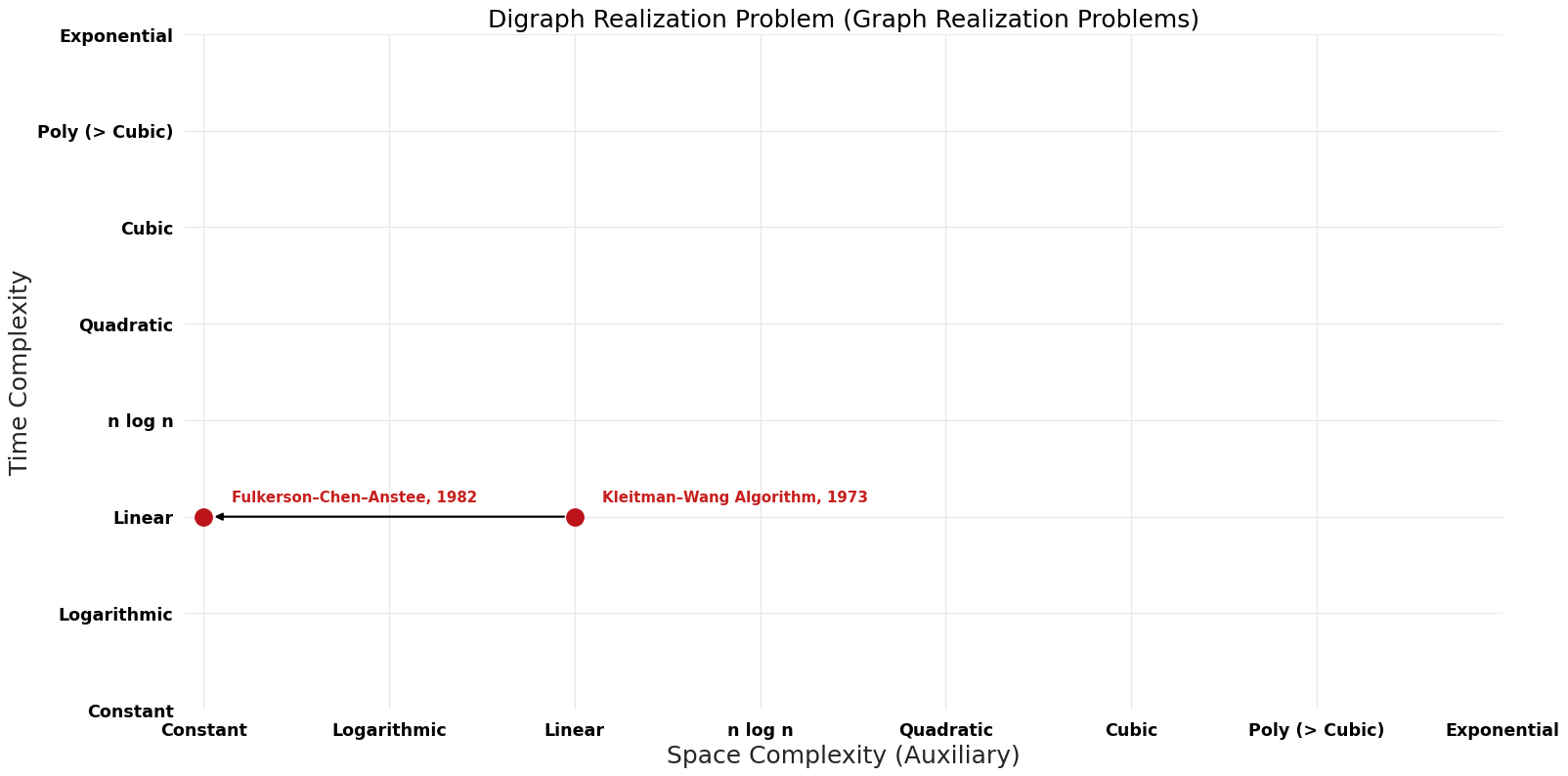
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Kleitman–Wang Algorithm | 1973 | $O(n)$ | $O(n)$ | Exact | Deterministic | Time |
| Fulkerson–Chen–Anstee | 1982 | $O(n)$ | $O({1})$ | Exact | Deterministic | Time |
Time Complexity Graph
Space Complexity Graph
Pareto Frontier Improvements Graph
References/Citation
https://linkinghub.elsevier.com/retrieve/pii/0012365X7390037X