Planar Bipartite Graph Perfect Matching (Maximum Cardinality Matching)
Revision as of 10:20, 15 February 2023 by Admin (talk | contribs) (Created page with "{{DISPLAYTITLE:Planar Bipartite Graph Perfect Matching (Maximum Cardinality Matching)}} == Description == The goal of maximum cardinality matching is to find a matching with as many edges as possible (equivalently: a matching that covers as many vertices as possible). Here, the graph is a planar bipartite graph. == Related Problems == Generalizations: Bipartite Graph MCM Related: General Graph MCM == Parameters == <pre>V: number of vertices E: number of...")
Description
The goal of maximum cardinality matching is to find a matching with as many edges as possible (equivalently: a matching that covers as many vertices as possible). Here, the graph is a planar bipartite graph.
Related Problems
Generalizations: Bipartite Graph MCM
Related: General Graph MCM
Parameters
V: number of vertices E: number of edges
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
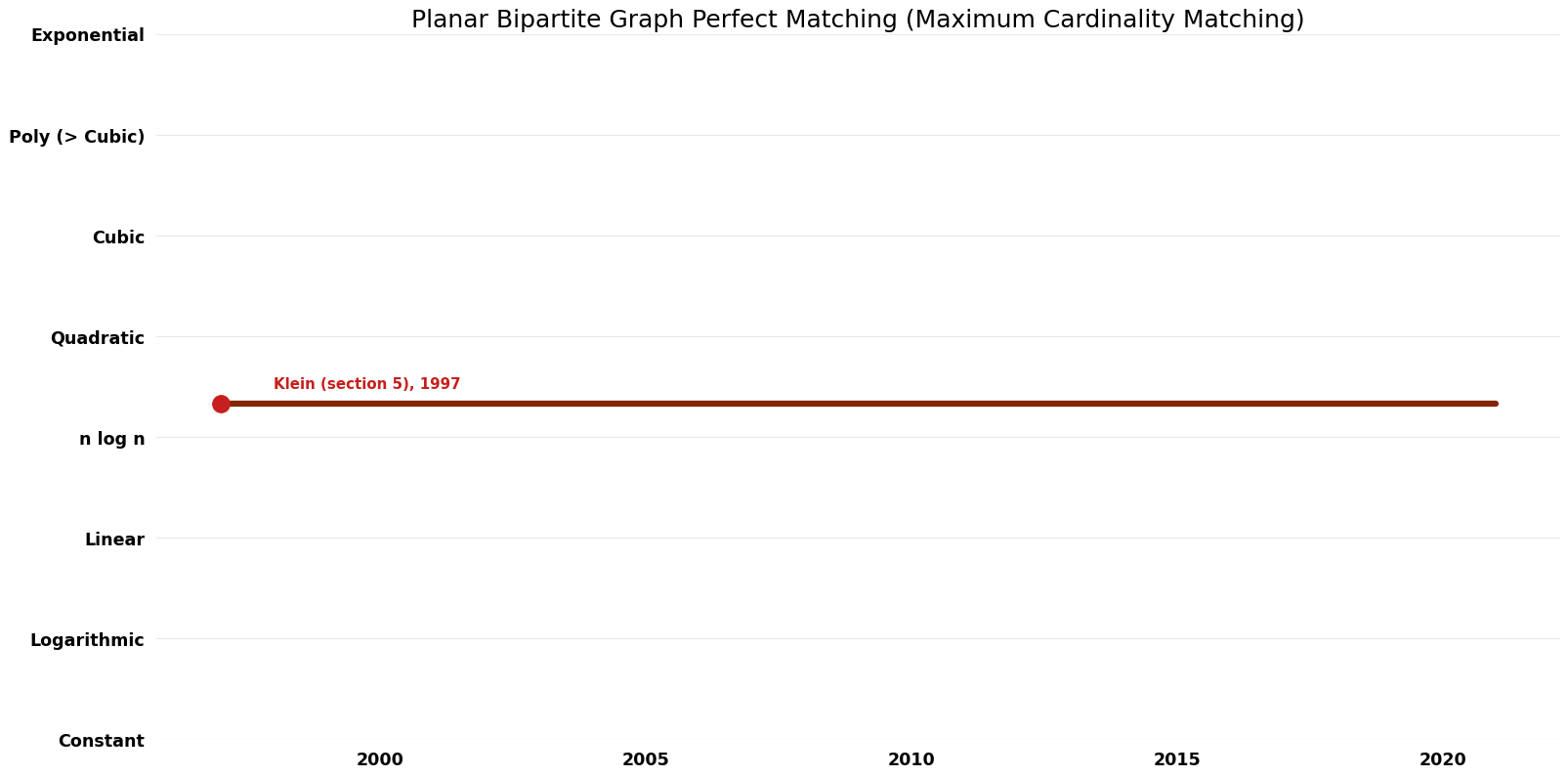
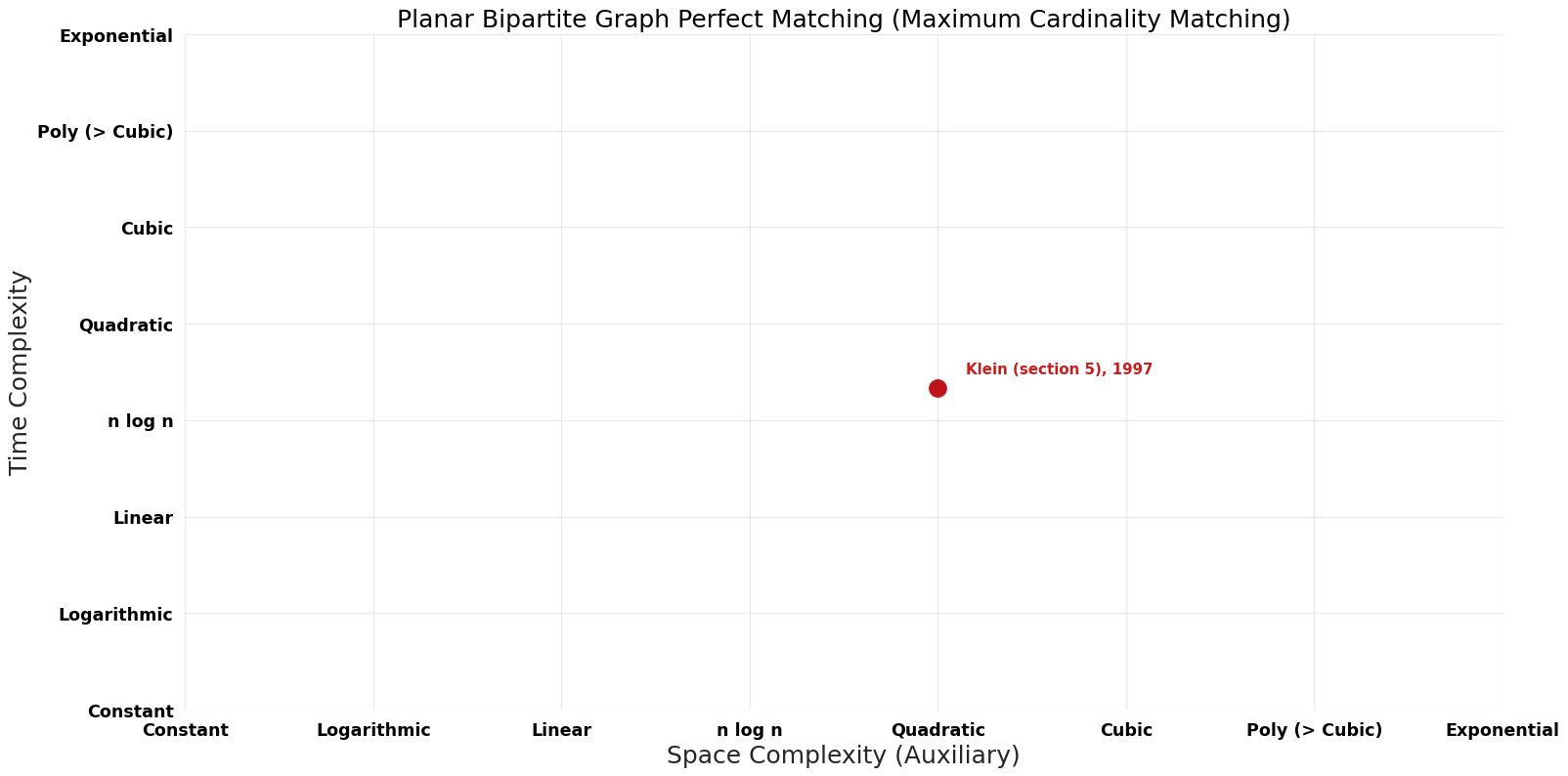
| Micali and Vazirani | 1980 | $O(V^{0.5} E)$ | $O(V)$ | Deterministic | Time & Space | |
| Klein (section 5) | 1997 | $O(V^{({4}/{3})$} logV) | $O(V^{({4}/{3})$})? | Exact | Deterministic | Time |
Time Complexity graph
Space Complexity graph
Pareto Decades graph
