Constructing Suffix Trees (Constructing Suffix Trees)

Description

Let $T = t_1 t_2 \cdots t_n, be a string over an alphabet $\Sigma$. Each string $x$ such that $T = uxv$ for some (possibly empty) strings $u$ and $v$ is a substring of $T$, and each string $T_i = t_i \cdots t_n$, where $1 \leq i \leq n + 1$ is a suffix of $T$; in particular, $T_{n+1} = \epsilon$ is the empty suffix. The set of all suffixes of $T$ is denoted $\sigma(T)$. The suffix trie $STrie(T)$ of $T$ is a trie representing $\sigma(T)$.

Suffix tree $STree(T)$ of $T$ is a data structure that represents $STrie(T)$ in space linear in the length $|T|$ of $T$. This is achieved by representing only a subset $Q' \cup \{ \perp \}$ of the states of $STrie(T)$.

Parameters

$n$: length of string

Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
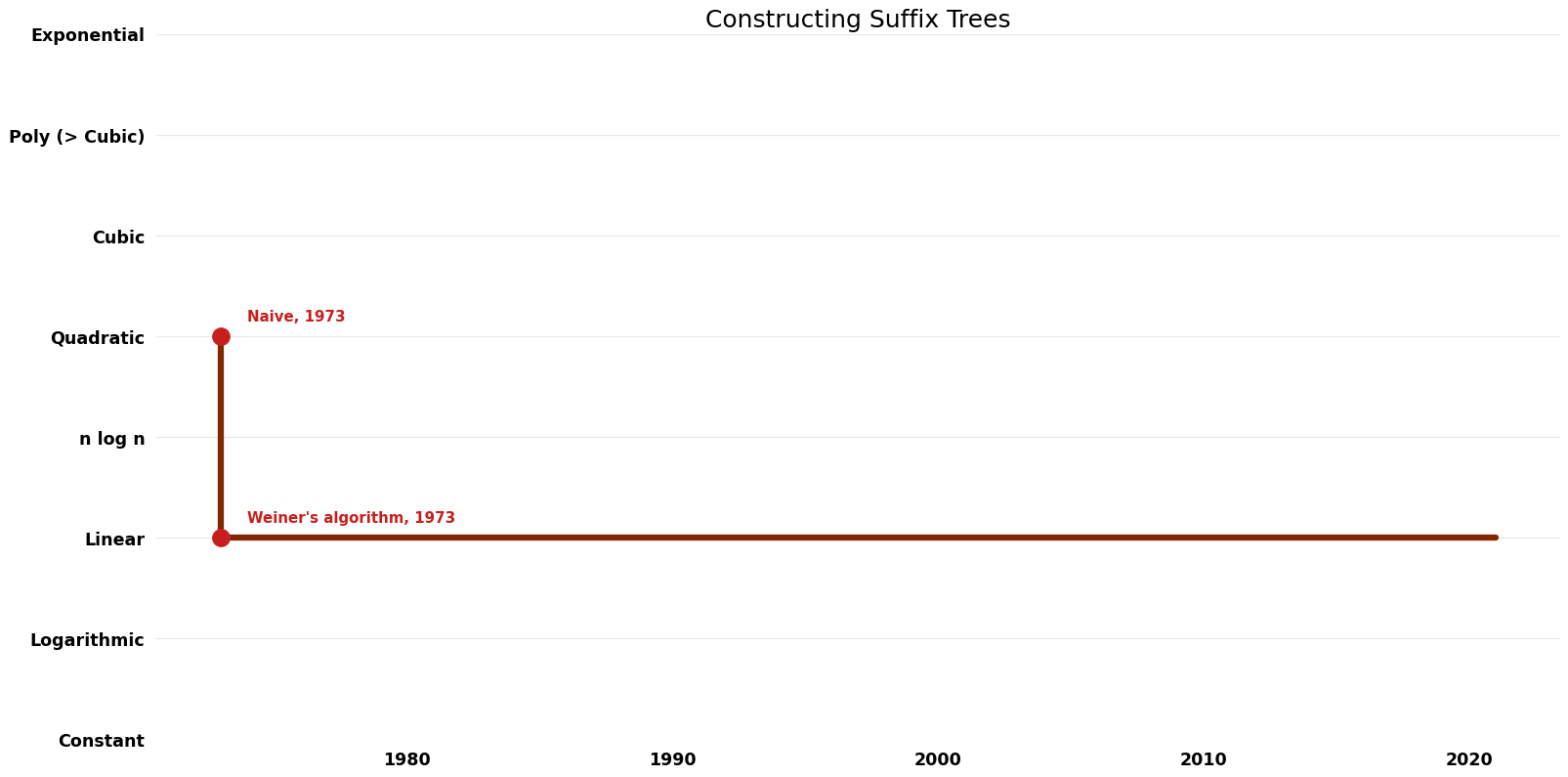
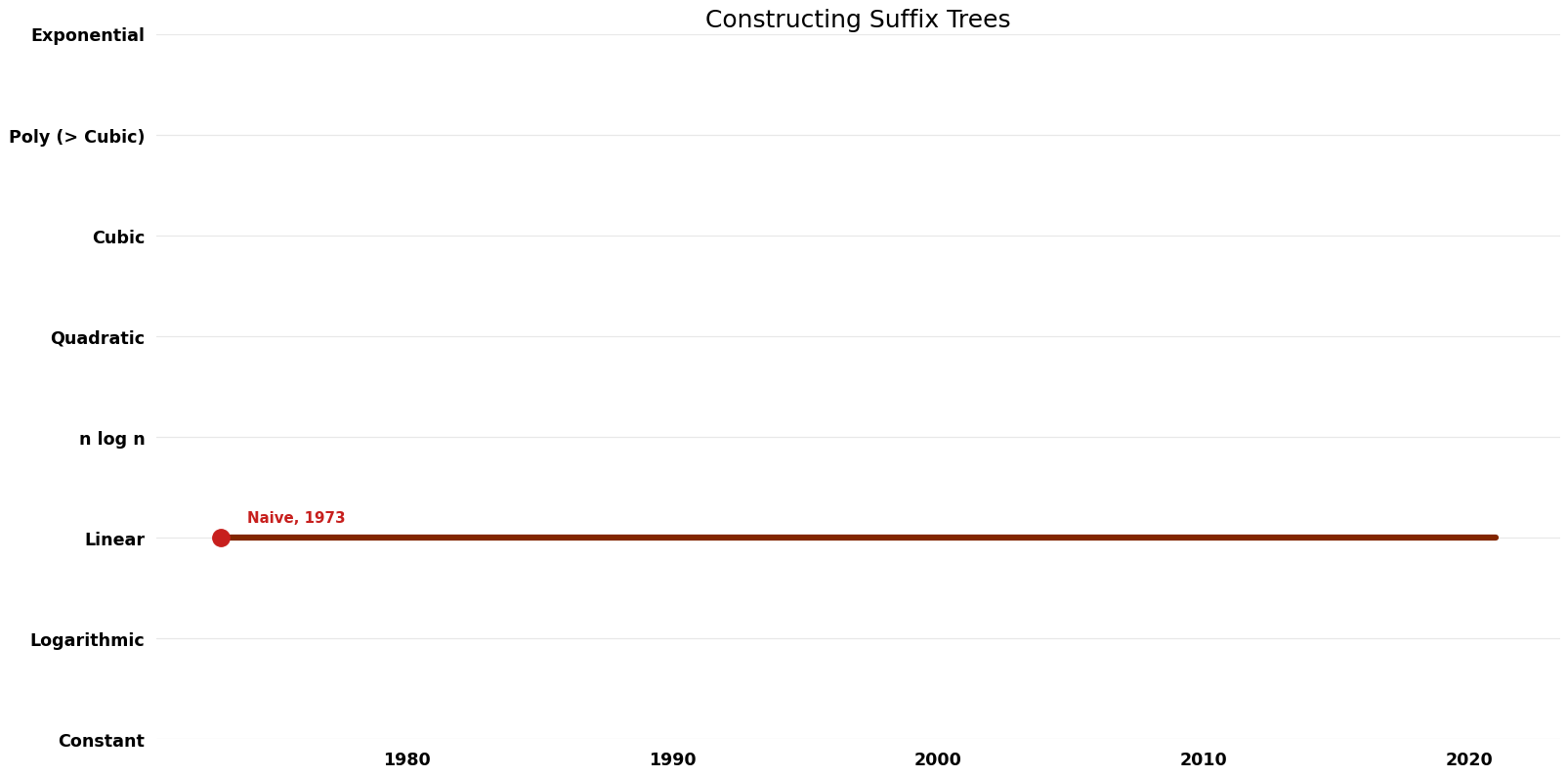
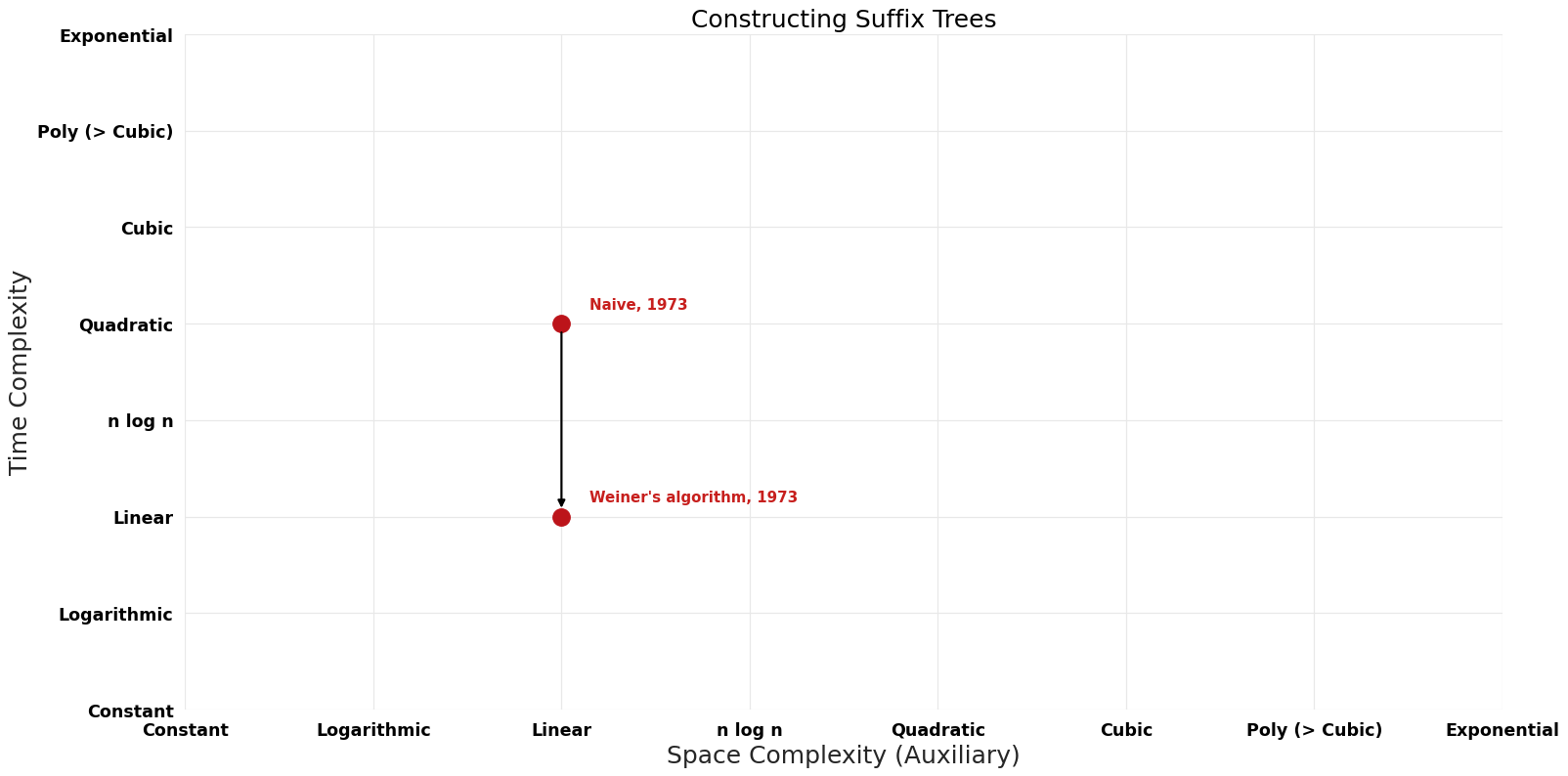
Naive	1973	$O(n^{2})$	$O(n)$	Exact	Deterministic
Weiner's algorithm	1973	$O(n)$	$O(n)$	Exact	Deterministic	Time
Pratt	1973	$O(n)$		Exact	Deterministic
Ukkonen	1995	$O(n)$	$O(n)$	Exact	Deterministic	Time
Ukkonen and D. Wood	1993	$O(n^{2})$	$O(n^{2})$	Exact	Deterministic	Time & Space
Hariharan	1997	$O(log^{4}(n)$)	$O(n)$	Exact	Parallel	Time & Space
Süleyman Cenk Sahinalp ; Uzi Vishkin	1994	$O(log^{2}(n)$)	$O(n^{({1}+\eps)})$ for any fixed eps>{0}	Exact	Parallel	Time & Space
Farach	1997	$O(\log n)$	$O(n)$	Exact	Randomized	Time & Space
Rytter	2004	$O(\log n)$	$O(n)$	Exact	Parallel	Time & Space
McCreight	1976	$O(n)$	$O(n)$	Exact	Deterministic	Time

Time Complexity Graph

Space Complexity Graph

Time-Space Tradeoff