Maximum Likelihood Methods in Unknown Latent Variables: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Maximum Likelihood Methods in Unknown Latent Variables (Maximum Likelihood Methods in Unknown Latent Variables)}} == Description == In this problem, the goal is to compute maximum-likelihood estimates when the observations can be viewed as incomplete data. == Parameters == No parameters found. == Table of Algorithms == {| class="wikitable sortable" style="text-align:center;" width="100%" ! Name !! Year !! Time !! Space !! Approximation Factor !!...") |
No edit summary |
||
| Line 27: | Line 27: | ||
|- | |- | ||
| [[α-EM Algorithm (Maximum Likelihood Methods in Unknown Latent Variables Maximum Likelihood Methods in Unknown Latent Variables)|α-EM Algorithm]] || 2003 || $O(n^{3})$ || $O(n+r)$? || Exact || Deterministic || [https://waseda.pure.elsevier.com/en/publications/the-%CE%B1-em-algorithm-surrogate-likelihood-maximization-using-%CE%B1-loga Time] | | [[α-EM Algorithm (Maximum Likelihood Methods in Unknown Latent Variables Maximum Likelihood Methods in Unknown Latent Variables)|α-EM Algorithm]] || 2003 || $O(n^{3})$ || $O(n+r)$? || Exact || Deterministic || [https://waseda.pure.elsevier.com/en/publications/the-%CE%B1-em-algorithm-surrogate-likelihood-maximization-using-%CE%B1-loga Time] | ||
|- | |||
| [[Shaban; Amirreza; Mehrdad; Farajtabar (Maximum Likelihood Methods in Unknown Latent Variables; multi-view model, discrete observations Maximum Likelihood Methods in Unknown Latent Variables)|Shaban; Amirreza; Mehrdad; Farajtabar]] || 2015 || $O(n^{2} log^{2} n)$ || $O(kd+d^{3})$?? || Exact || Deterministic || [https://faculty.cc.gatech.edu/~bboots3/files/SpectralExteriorPoint-NIPSWorkshop.pdf Time] | |||
|- | |||
| [[alpha-HMM (Matsuyama, Yasuo) (Maximum Likelihood Methods in Unknown Latent Variables, Hidden Markov Models Maximum Likelihood Methods in Unknown Latent Variables)|alpha-HMM (Matsuyama, Yasuo)]] || 2011 || $O(n^{2} log^{2} n)$ || || Exact || Deterministic || [https://ieeexplore.ieee.org/abstract/document/7895145 Time] | |||
|- | |- | ||
|} | |} | ||
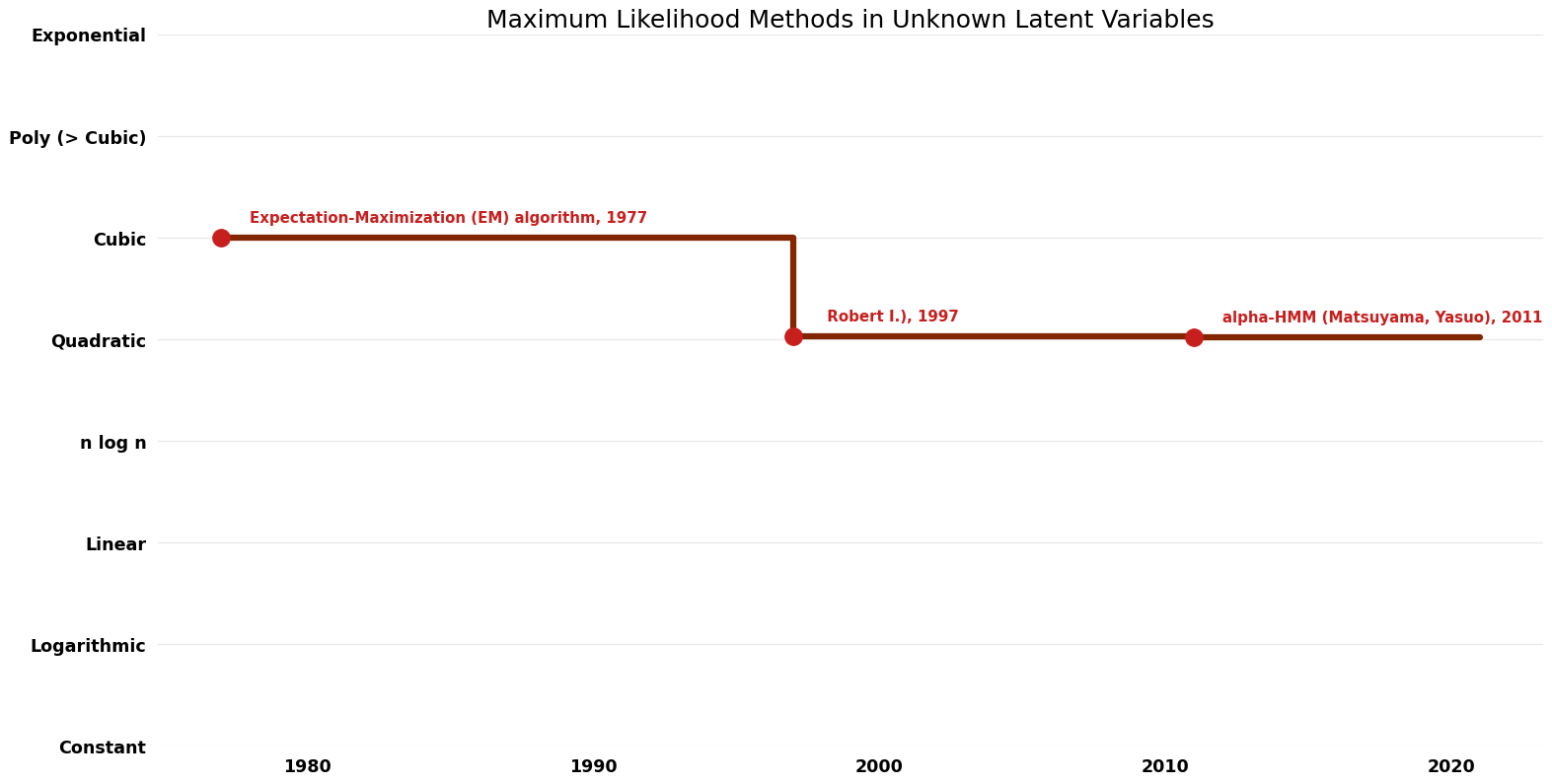
== Time Complexity | == Time Complexity Graph == | ||
[[File:Maximum Likelihood Methods in Unknown Latent Variables - Time.png|1000px]] | [[File:Maximum Likelihood Methods in Unknown Latent Variables - Time.png|1000px]] | ||
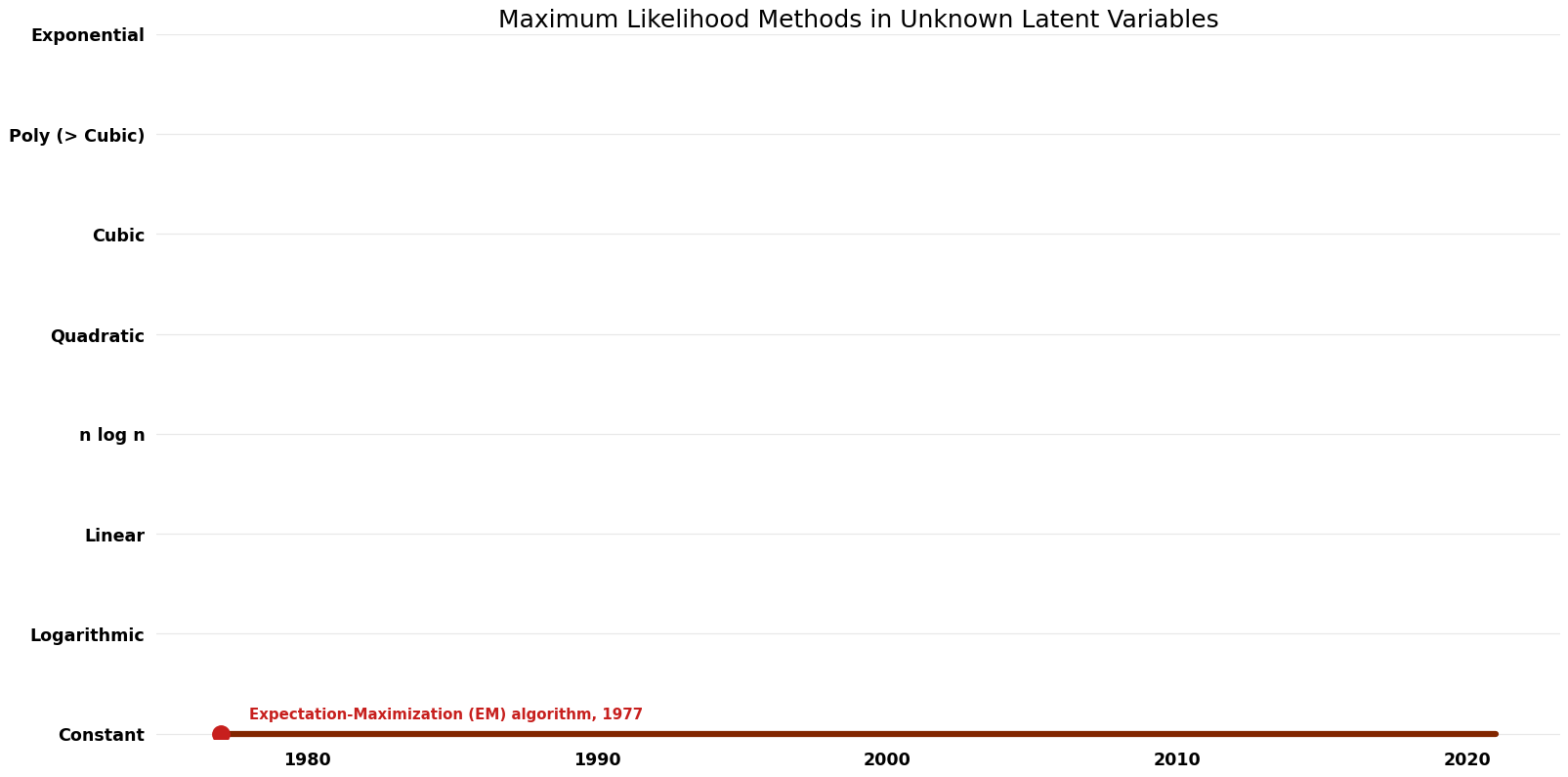
== Space Complexity | == Space Complexity Graph == | ||
[[File:Maximum Likelihood Methods in Unknown Latent Variables - Space.png|1000px]] | [[File:Maximum Likelihood Methods in Unknown Latent Variables - Space.png|1000px]] | ||
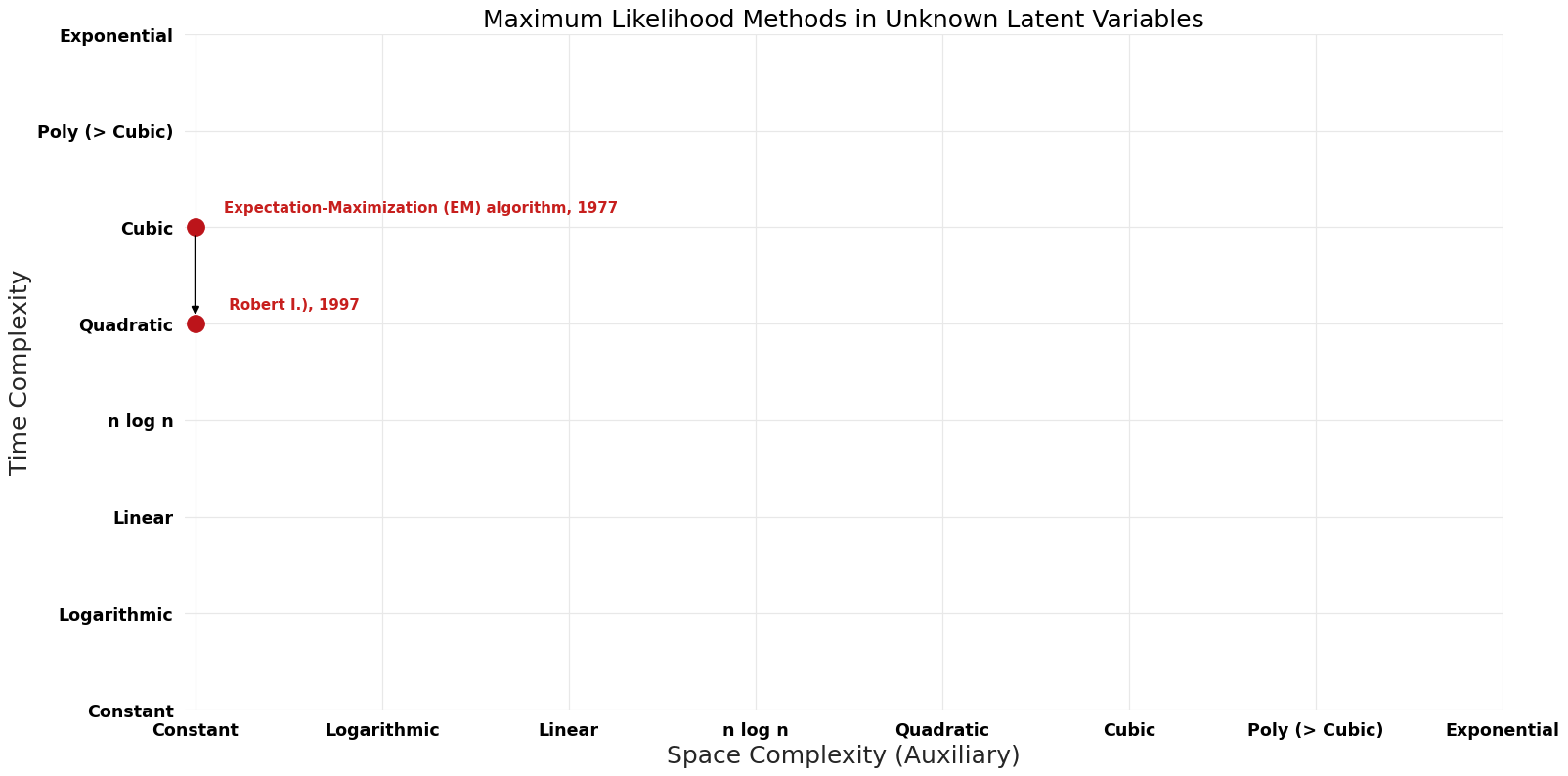
== Pareto | == Pareto Frontier Improvements Graph == | ||
[[File:Maximum Likelihood Methods in Unknown Latent Variables - Pareto Frontier.png|1000px]] | [[File:Maximum Likelihood Methods in Unknown Latent Variables - Pareto Frontier.png|1000px]] | ||
Revision as of 13:04, 15 February 2023
Description
In this problem, the goal is to compute maximum-likelihood estimates when the observations can be viewed as incomplete data.
Parameters
No parameters found.
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Expectation-Maximization (EM) algorithm | 1977 | $O(n^{3})$ | $O(n+r)$? | Exact | Deterministic | Time |
| EM with Quasi-Newton Methods (Jamshidian; Mortaza; Jennrich; Robert I.) | 1997 | $O(n^{2} log^{3} n)$ | $O(n+r^{2})$? | Exact | Deterministic | Time |
| Parameter-expanded expectation maximization (PX-EM) | 1998 | $O(n^{3})$ | $O(n+r)$? | Exact | Deterministic | Time |
| Expectation conditional maximization (ECM) | 1993 | $O(n^{3})$ | $O(n+r)$? | Exact | Deterministic | Time |
| Expectation conditional maximization either (ECME) (Liu; Chuanhai; Rubin; Donald B) | 1994 | $O(n^{3})$ | $O(n+r)$? | Exact | Deterministic | Time |
| α-EM Algorithm | 2003 | $O(n^{3})$ | $O(n+r)$? | Exact | Deterministic | Time |
| Shaban; Amirreza; Mehrdad; Farajtabar | 2015 | $O(n^{2} log^{2} n)$ | $O(kd+d^{3})$?? | Exact | Deterministic | Time |
| alpha-HMM (Matsuyama, Yasuo) | 2011 | $O(n^{2} log^{2} n)$ | Exact | Deterministic | Time |
Time Complexity Graph
Space Complexity Graph
Pareto Frontier Improvements Graph
