Maximum-Weight Matching: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 24: | Line 24: | ||
|- | |- | ||
| [[Hungarian algorithm (Bipartite Maximum-Weight Matching Maximum-Weight Matching)|Hungarian algorithm]] || 1955 || $O(n^{4})$ || $O(n^{2})$ || Exact || Deterministic || [https://web.eecs.umich.edu/~pettie/matching/Kuhn-hungarian-assignment.pdf Time] | |||
|- | |||
| [[Edmonds (Maximum-Weight Matching Maximum-Weight Matching)|Edmonds]] || 1965 || $O(mn^{2})$ || $O(mn^{2})$?? || Exact || Deterministic || [https://nvlpubs.nist.gov/nistpubs/jres/69B/jresv69Bn1-2p125_A1b.pdf Time] | | [[Edmonds (Maximum-Weight Matching Maximum-Weight Matching)|Edmonds]] || 1965 || $O(mn^{2})$ || $O(mn^{2})$?? || Exact || Deterministic || [https://nvlpubs.nist.gov/nistpubs/jres/69B/jresv69Bn1-2p125_A1b.pdf Time] | ||
|- | |- | ||
| Line 32: | Line 34: | ||
|} | |} | ||
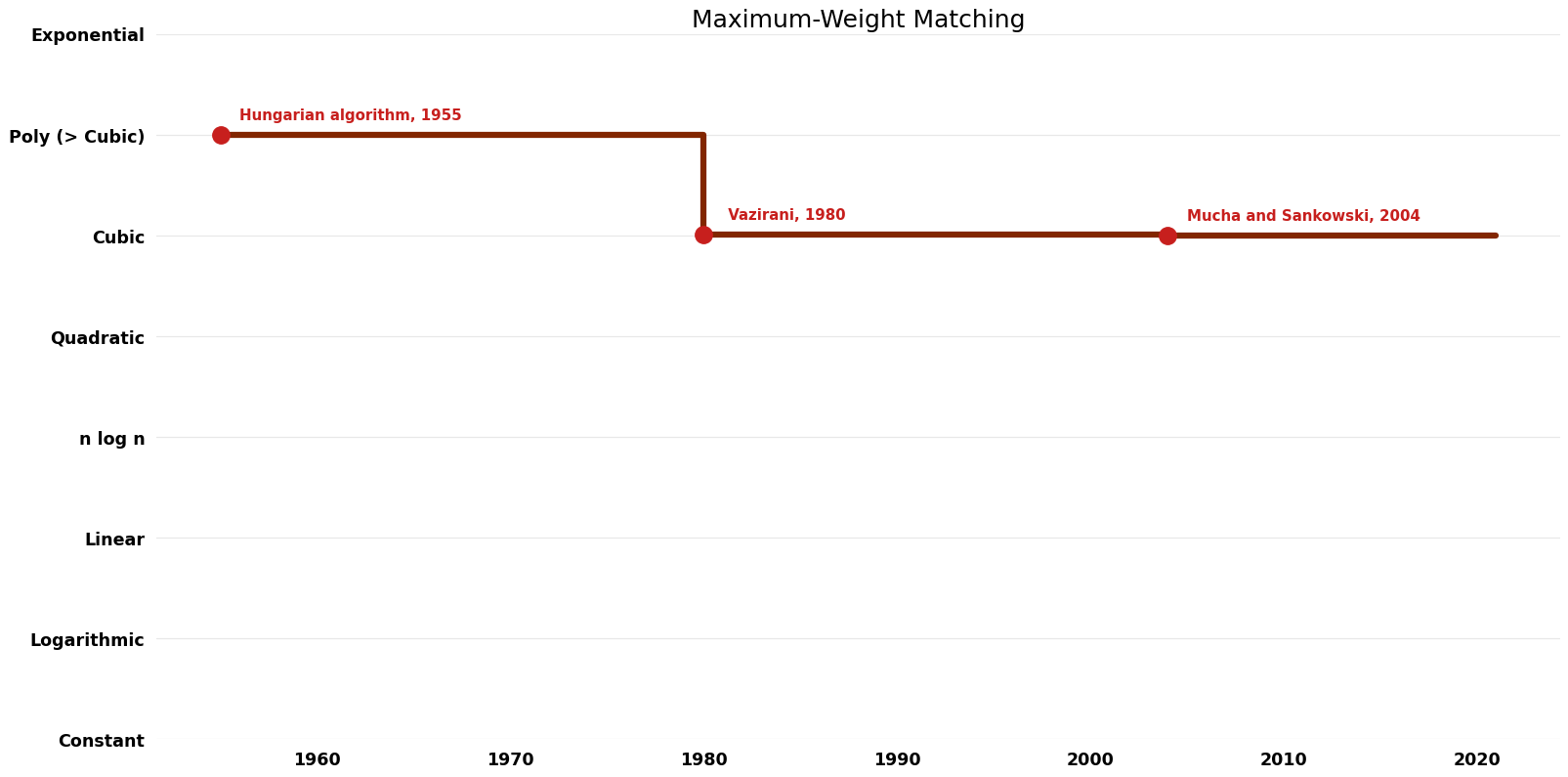
== Time Complexity | == Time Complexity Graph == | ||
[[File:Maximum-Weight Matching - Time.png|1000px]] | [[File:Maximum-Weight Matching - Time.png|1000px]] | ||
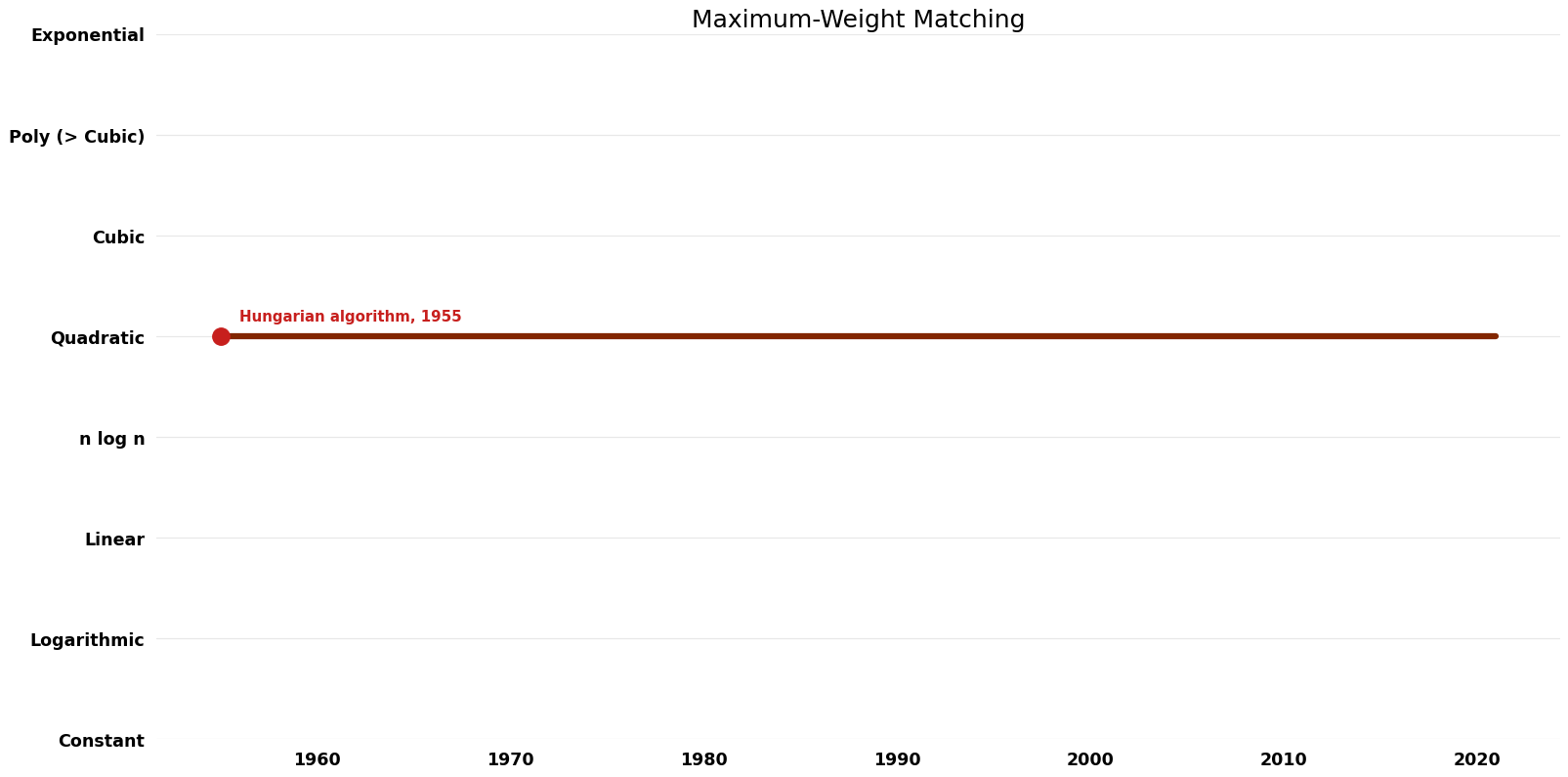
== Space Complexity | == Space Complexity Graph == | ||
[[File:Maximum-Weight Matching - Space.png|1000px]] | [[File:Maximum-Weight Matching - Space.png|1000px]] | ||
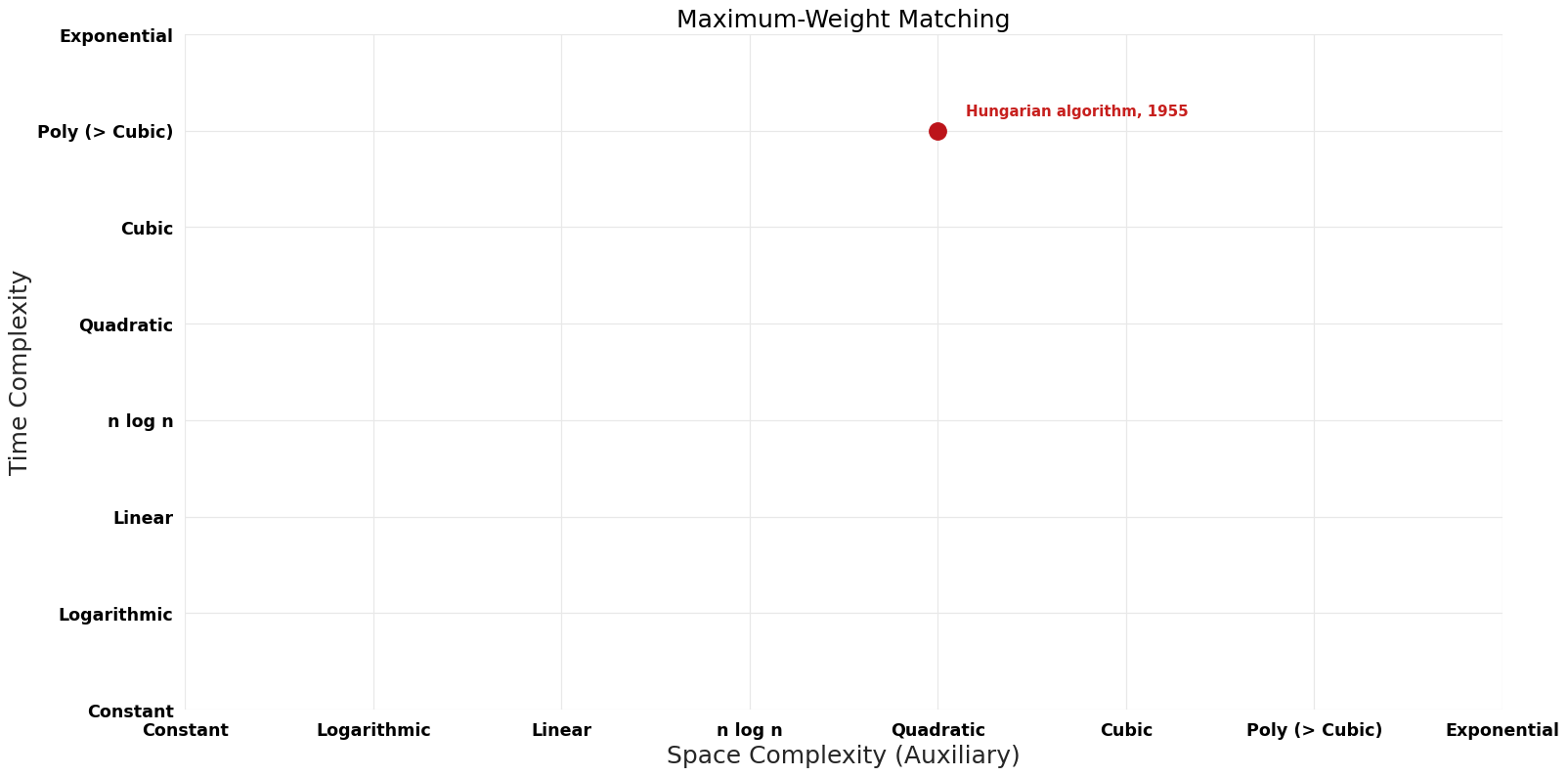
== Pareto | == Pareto Frontier Improvements Graph == | ||
[[File:Maximum-Weight Matching - Pareto Frontier.png|1000px]] | [[File:Maximum-Weight Matching - Pareto Frontier.png|1000px]] | ||
Revision as of 13:04, 15 February 2023
Description
In computer science, the maximum weight matching problem is the problem of finding, in a weighted graph, a matching in which the sum of weights is maximized. Here, the graph is unrestricted; i.e. can be any general graph.
Related Problems
Subproblem: Bipartite Maximum-Weight Matching
Parameters
n: number of vertices
m: number of edges
N: largest weight magnitude
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Hungarian algorithm | 1955 | $O(n^{4})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Edmonds | 1965 | $O(mn^{2})$ | $O(mn^{2})$?? | Exact | Deterministic | Time |
| Micali; Vazirani | 1980 | $O(n^{3} logn)$ | Exact | Deterministic | Time | |
| Mucha and Sankowski | 2004 | $O(n^{3})$ | Exact | Deterministic | Time |
Time Complexity Graph
Space Complexity Graph
Pareto Frontier Improvements Graph
