2-dimensional space, Euclidean metric: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:2-dimensional space, Euclidean metric (Closest Pair Problem)}} == Description == Given $n$ points in 2-dimensional space equipped with the Eucildean metric, find a pair of points with the smallest distance between them. == Related Problems == Related: k-dimensional space, $l_m$ (or $l_\infty$) norm, 2-dimensional space, $l_m$ (or $l_\infty$) norm, 2-dimensional array representation == Parameters == No parameters found. == Table of Alg...") |
No edit summary |
||
| Line 26: | Line 26: | ||
|} | |} | ||
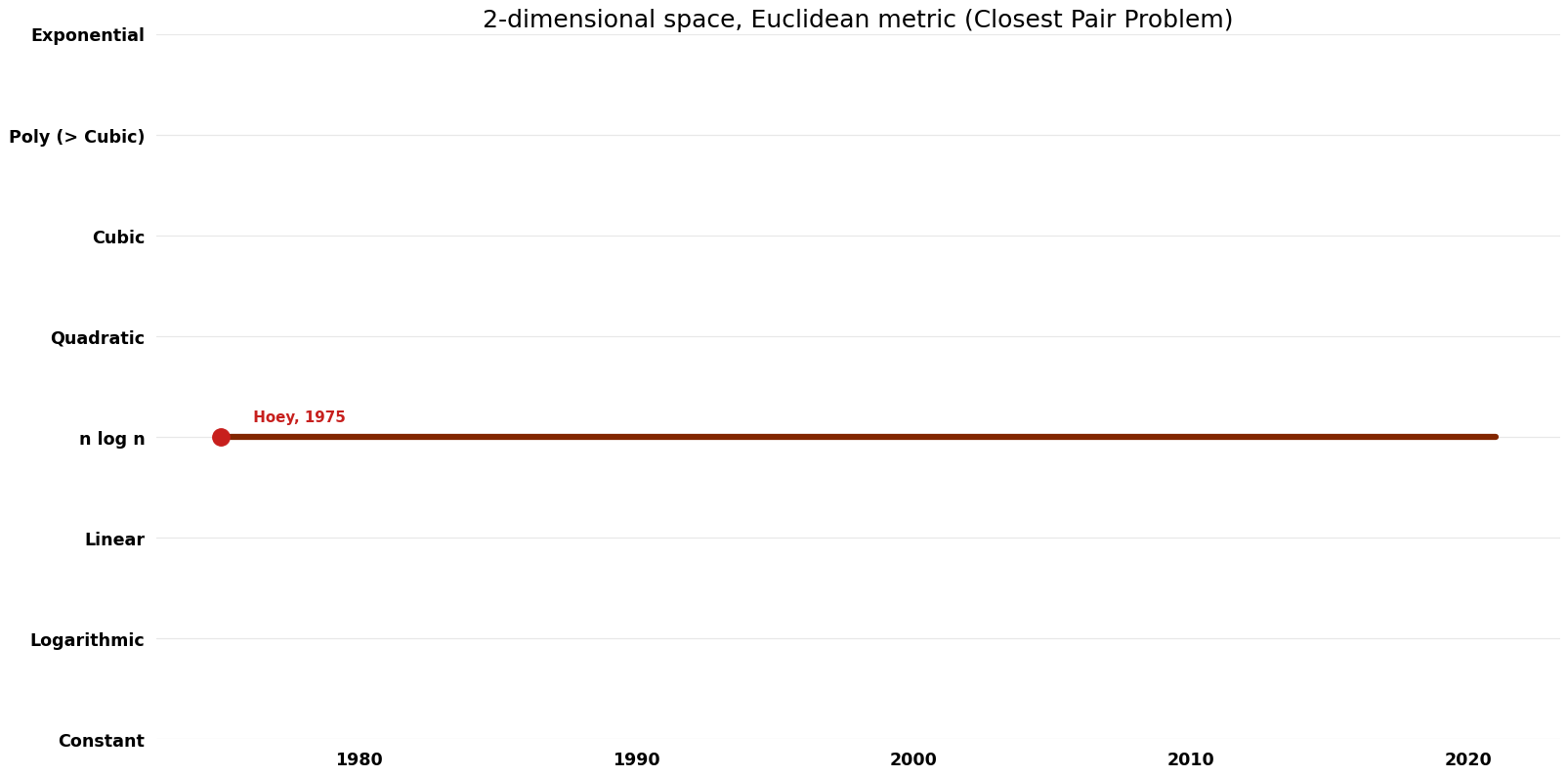
== Time Complexity | == Time Complexity Graph == | ||
[[File:Closest Pair Problem - 2-dimensional space, Euclidean metric - Time.png|1000px]] | [[File:Closest Pair Problem - 2-dimensional space, Euclidean metric - Time.png|1000px]] | ||
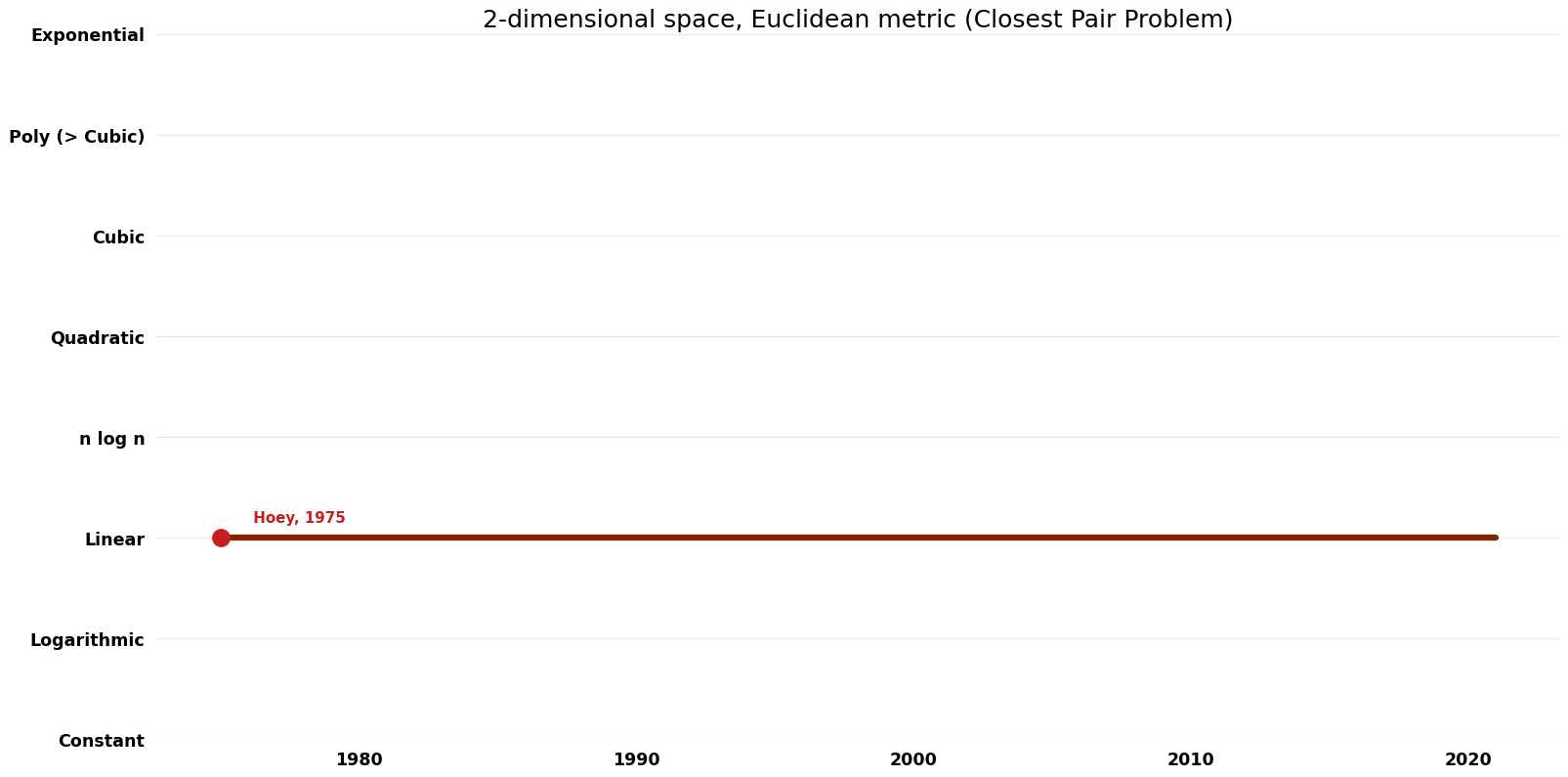
== Space Complexity | == Space Complexity Graph == | ||
[[File:Closest Pair Problem - 2-dimensional space, Euclidean metric - Space.png|1000px]] | [[File:Closest Pair Problem - 2-dimensional space, Euclidean metric - Space.png|1000px]] | ||
== Pareto | == Pareto Frontier Improvements Graph == | ||
[[File:Closest Pair Problem - 2-dimensional space, Euclidean metric - Pareto Frontier.png|1000px]] | [[File:Closest Pair Problem - 2-dimensional space, Euclidean metric - Pareto Frontier.png|1000px]] | ||
Revision as of 13:04, 15 February 2023
Description
Given $n$ points in 2-dimensional space equipped with the Eucildean metric, find a pair of points with the smallest distance between them.
Related Problems
Related: k-dimensional space, $l_m$ (or $l_\infty$) norm, 2-dimensional space, $l_m$ (or $l_\infty$) norm, 2-dimensional array representation
Parameters
No parameters found.
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Khuller; Matias Randomized Sieve | 1995 | $O(n)$ | $O(n)$, not sure if this is auxiliary | Exact | Randomized | Time & Space |
| Shamos; Hoey | 1975 | $O(n logn)$ | $O(n)$ | Exact | Deterministic | Time |
Time Complexity Graph
Space Complexity Graph
Pareto Frontier Improvements Graph
