Maximum-Weight Matching: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 37: | Line 37: | ||
[[File:Maximum-Weight Matching - Time.png|1000px]] | [[File:Maximum-Weight Matching - Time.png|1000px]] | ||
Latest revision as of 09:08, 28 April 2023
Description
In computer science, the maximum weight matching problem is the problem of finding, in a weighted graph, a matching in which the sum of weights is maximized. Here, the graph is unrestricted; i.e. can be any general graph.
Related Problems
Subproblem: Bipartite Maximum-Weight Matching
Parameters
$n$: number of vertices
$m$: number of edges
$N$: largest weight magnitude
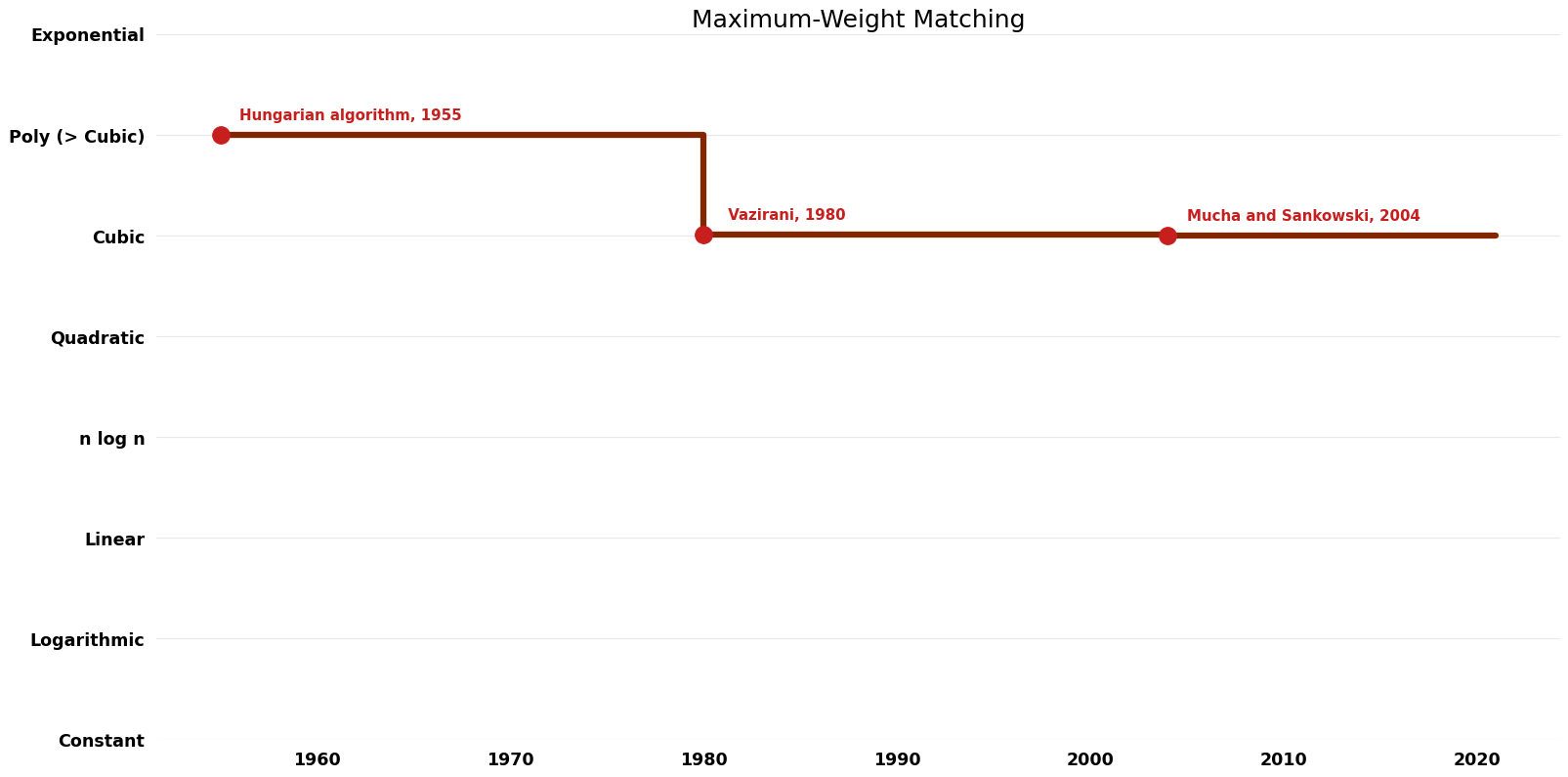
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Hungarian algorithm | 1955 | $O(n^{4})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Edmonds | 1965 | $O(mn^{2})$ | $O(mn^{2})$?? | Exact | Deterministic | Time |
| Micali; Vazirani | 1980 | $O(n^{3} \log n)$ | Exact | Deterministic | Time | |
| Mucha and Sankowski | 2004 | $O(n^{3})$ | Exact | Deterministic | Time |
Time Complexity Graph
