Hyperbolic Spline Interpolation: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Hyperbolic Spline Interpolation (Hyperbolic Spline Interpolation)}} == Description == The problem of restoring complex curves and surfaces from discrete data so that their shape is preserved is called isogeometric interpolation. A very popular tool for solving this problem are hyperbolic splines in tension, which were introduced in 1966 by Schweikert. These splines have smoothness sufficient for many applications; combined with algorithms for the automat...") |
No edit summary |
||
| Line 30: | Line 30: | ||
|} | |} | ||
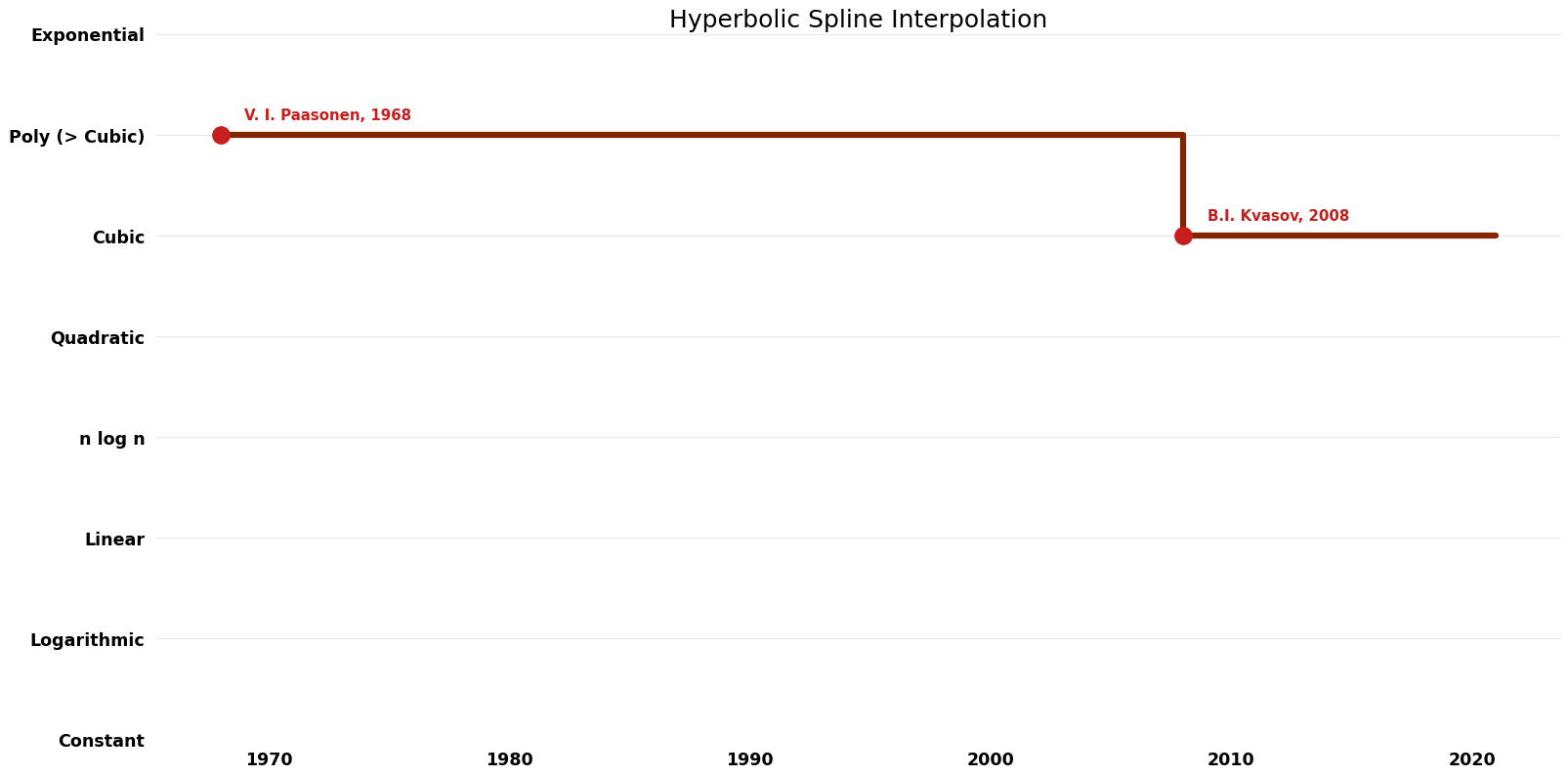
== Time Complexity | == Time Complexity Graph == | ||
[[File:Hyperbolic Spline Interpolation - Time.png|1000px]] | [[File:Hyperbolic Spline Interpolation - Time.png|1000px]] | ||
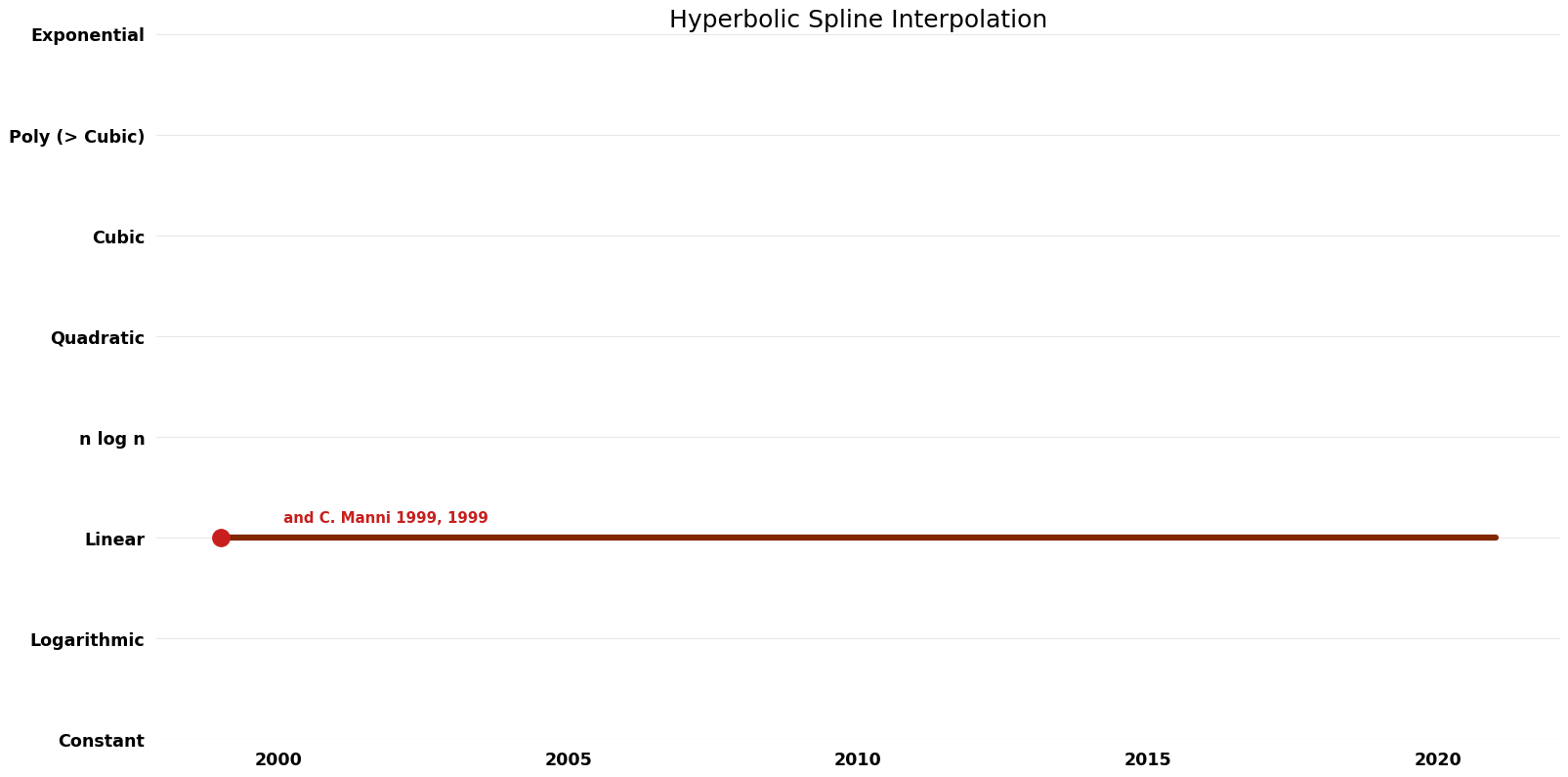
== Space Complexity | == Space Complexity Graph == | ||
[[File:Hyperbolic Spline Interpolation - Space.png|1000px]] | [[File:Hyperbolic Spline Interpolation - Space.png|1000px]] | ||
== Pareto | == Pareto Frontier Improvements Graph == | ||
[[File:Hyperbolic Spline Interpolation - Pareto Frontier.png|1000px]] | [[File:Hyperbolic Spline Interpolation - Pareto Frontier.png|1000px]] | ||
Revision as of 13:04, 15 February 2023
Description
The problem of restoring complex curves and surfaces from discrete data so that their shape is preserved is called isogeometric interpolation. A very popular tool for solving this problem are hyperbolic splines in tension, which were introduced in 1966 by Schweikert. These splines have smoothness sufficient for many applications; combined with algorithms for the automatic selection of the tension parameters, they adapt well to the given data. Unfortunately, the evaluation of hyperbolic splines is a very difficult problem because of roundoff errors (for small values of the tension parameters) and overflows (for large values of these parameters).�
Parameters
No parameters found.
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Kvasov 2006 | 2008 | $O(n^{3} log^{2}K)$ | Exact | Deterministic | Time | |
| V. A. Lyul’ka and A. V. Romanenko | 1994 | $O(n^{5})$ | Exact | Deterministic | Time | |
| V. A. Lyul’ka and I. E. Mikhailov | 2003 | $O(n^{4})$ | Exact | Deterministic | Time | |
| V. I. Paasonen | 1968 | $O(n^{5} logK)$ | Exact | Deterministic | ||
| P. Costantini; B. I. Kvasov; and C. Manni | 1999 | $O(n^{5} logK)$ | $O(n)$? | Exact | Deterministic | Time |
| B. I. Kvasov | 2000 | $O(n^{4})$ | Exact | Deterministic |
Time Complexity Graph
Space Complexity Graph
Pareto Frontier Improvements Graph
