Entity Resolution: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 39: | Line 39: | ||
[[File:Entity Resolution - Time.png|1000px]] | [[File:Entity Resolution - Time.png|1000px]] | ||
Latest revision as of 10:10, 28 April 2023
Description
Entity resolution (ER) is the problem of matching records that represent the same real-world entity and then merging the matching records. ER is a well known problem that arises in many applications. An exhaustive ER process involves comparing all the pairs of records, which can be very expensive for large datasets.
Parameters
$n$: number of records
$k$: number of features
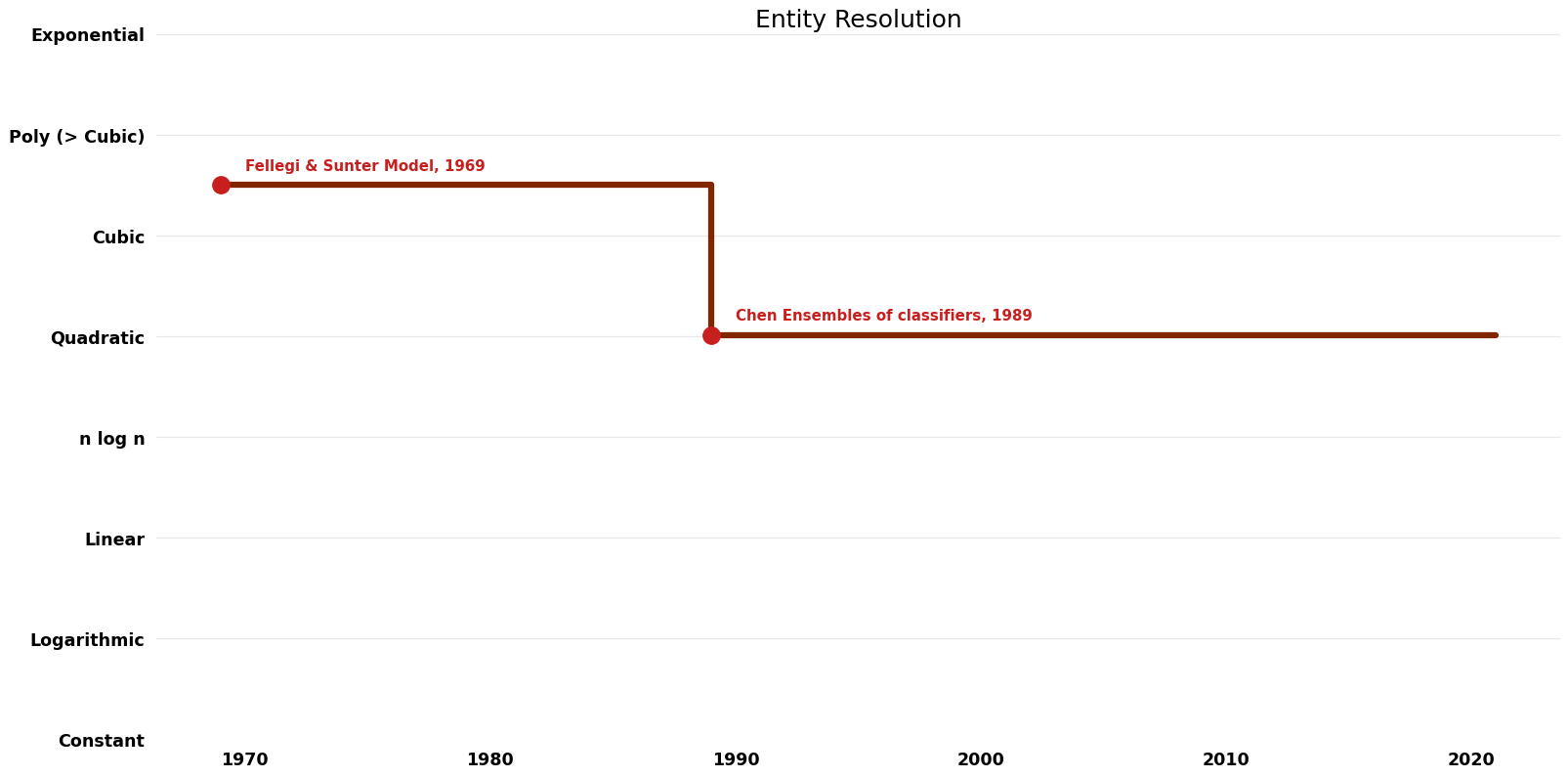
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Fellegi & Sunter Model | 1969 | $O(n^{3}k)$ | $O(k)$ | Exact | Deterministic | Time |
| Gupta & Sarawagi CRF | 2009 | $O(n^{3}k)$ | $O(nk)$? | Exact | Deterministic | Time |
| Chen Ensembles of classifiers | 1989 | $O(n^{2} \log n)$ | Exact | Deterministic | ||
| EM Based Winkler | 2000 | $O(n^{3}k)$ | $O(k)$ | Exact | Deterministic | Time |
| Ravikumar & Cohen Generative Models | 2004 | $O(n^{2} k)$ | $O(k)$ | Exact | Deterministic | Time |
| Bellare Active Learning | 2012 | $O(n^{2} \log n c \log c)$ | Exact | Deterministic | Time | |
| Ananthakrishna | 2002 | $O(n^{2} k)$ | $O(n)$ | Exact | Deterministic | Time |
| BOYS algorithm | 1993 | $O(n^{2} k)$ | $O(n^{2})$ | Exact | Deterministic | Time |