Hyperbolic Spline Interpolation: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
$n$: number of points | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 16: | Line 16: | ||
|- | |- | ||
| [[Kvasov | | [[B.I. Kvasov (Hyperbolic Spline Interpolation Hyperbolic Spline Interpolation)|B.I. Kvasov]] || 2008 || $O(n^{3} \log^{2}K)$ || $O(n)$? || Exact || Deterministic || [https://link.springer.com/article/10.1134/S0965542508040039 Time] | ||
|- | |- | ||
| [[V. A. Lyul’ka and A. V. Romanenko | | [[V. A. Lyul’ka and A. V. Romanenko (Hyperbolic Spline Interpolation Hyperbolic Spline Interpolation)|V. A. Lyul’ka and A. V. Romanenko]] || 1994 || $O(n^{5})$ || || Exact || Deterministic || [https://www.mathnet.ru/eng/zvmmf2544 Time] | ||
|- | |- | ||
| [[V. A. Lyul’ka and I. E. Mikhailov | | [[V. A. Lyul’ka and I. E. Mikhailov (Hyperbolic Spline Interpolation Hyperbolic Spline Interpolation)|V. A. Lyul’ka and I. E. Mikhailov]] || 2003 || $O(n^{4})$ || || Exact || Deterministic || [http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=zvmmf&paperid=943&option_lang=eng Time] | ||
|- | |- | ||
| [[V. I. Paasonen | | [[V. I. Paasonen (Hyperbolic Spline Interpolation Hyperbolic Spline Interpolation)|V. I. Paasonen]] || 1968 || $O(n^{5} \log K)$ || || Exact || Deterministic || | ||
|- | |- | ||
| [[P. Costantini | | [[P. Costantini, B. I. Kvasov, and C. Manni (Hyperbolic Spline Interpolation Hyperbolic Spline Interpolation)|P. Costantini, B. I. Kvasov, and C. Manni]] || 1999 || $O(n^{5} \log K)$ || $O(n)$? || Exact || Deterministic || [https://link.springer.com/article/10.1023/A:1018988312596 Time] | ||
|- | |- | ||
| [[B. I. Kvasov | | [[B. I. Kvasov (Hyperbolic Spline Interpolation Hyperbolic Spline Interpolation)|B. I. Kvasov]] || 2000 || $O(n^{4})$ || $O(n)$?? || Exact || Deterministic || [http://sutir.sut.ac.th:8080/sutir/bitstream/123456789/431/1/bib115.pdf Time] | ||
|- | |- | ||
|} | |} | ||
| Line 33: | Line 33: | ||
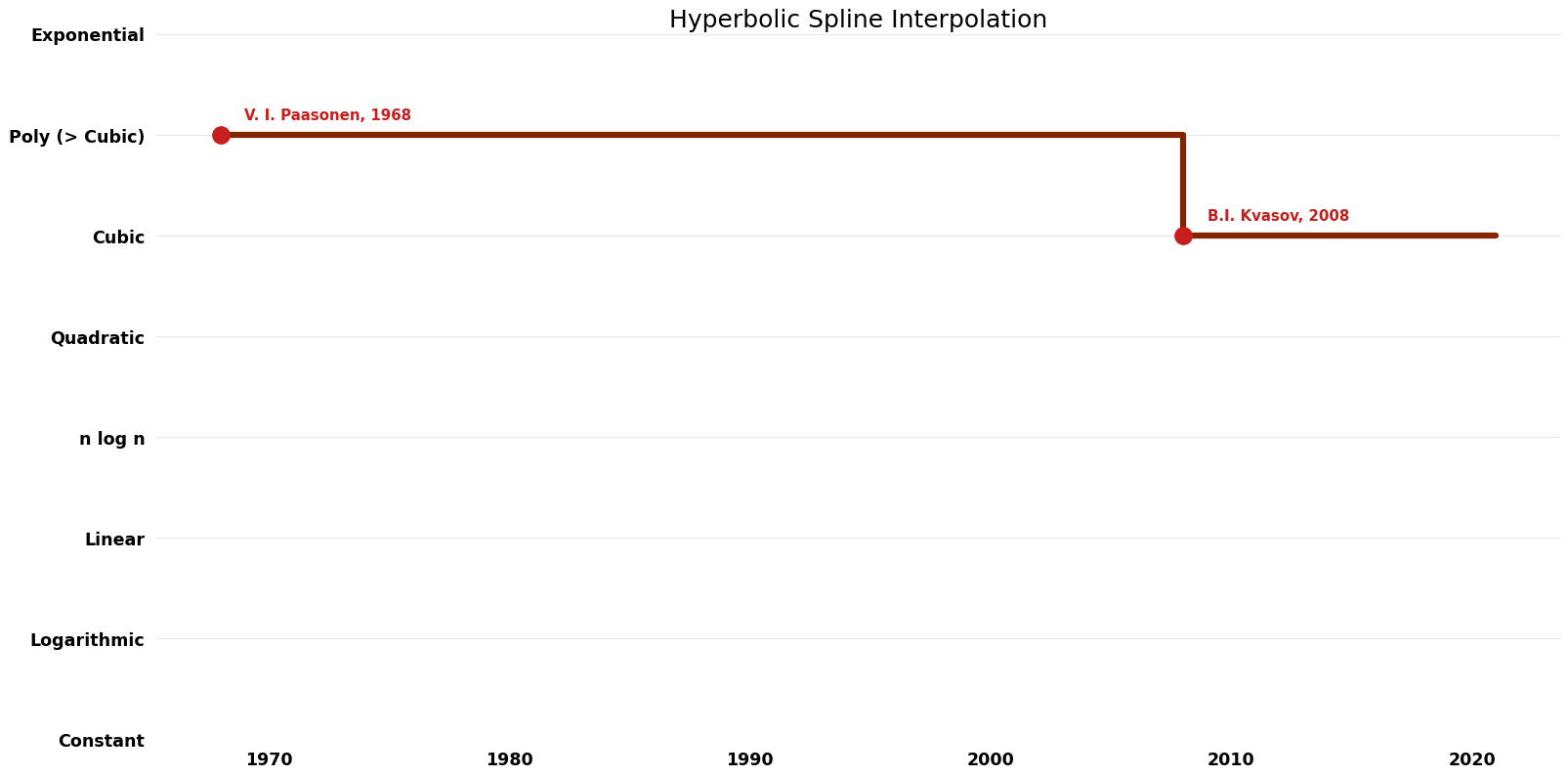
[[File:Hyperbolic Spline Interpolation - Time.png|1000px]] | [[File:Hyperbolic Spline Interpolation - Time.png|1000px]] | ||
Latest revision as of 10:10, 28 April 2023
Description
The problem of restoring complex curves and surfaces from discrete data so that their shape is preserved is called isogeometric interpolation. A very popular tool for solving this problem are hyperbolic splines in tension, which were introduced in 1966 by Schweikert. These splines have smoothness sufficient for many applications; combined with algorithms for the automatic selection of the tension parameters, they adapt well to the given data. Unfortunately, the evaluation of hyperbolic splines is a very difficult problem because of roundoff errors (for small values of the tension parameters) and overflows (for large values of these parameters).�
Parameters
$n$: number of points
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| B.I. Kvasov | 2008 | $O(n^{3} \log^{2}K)$ | $O(n)$? | Exact | Deterministic | Time |
| V. A. Lyul’ka and A. V. Romanenko | 1994 | $O(n^{5})$ | Exact | Deterministic | Time | |
| V. A. Lyul’ka and I. E. Mikhailov | 2003 | $O(n^{4})$ | Exact | Deterministic | Time | |
| V. I. Paasonen | 1968 | $O(n^{5} \log K)$ | Exact | Deterministic | ||
| P. Costantini, B. I. Kvasov, and C. Manni | 1999 | $O(n^{5} \log K)$ | $O(n)$? | Exact | Deterministic | Time |
| B. I. Kvasov | 2000 | $O(n^{4})$ | $O(n)$?? | Exact | Deterministic | Time |