Lossy Compression: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Lossy Compression (Data Compression)}} == Description == The reduction or ideally elimination of redundancies in the original data to result in smaller required storage space is the goal of every compression scheme. There are two categories of data compression: lossy and lossless. Lossy compression is achieved by only discarding the redundancies and out of human perception information and getting rid of those extra bits. == Related Problems == Relat...") |
No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
== Parameters == | == Parameters == | ||
$n$: number of items in input series of data | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 28: | Line 28: | ||
| [[Maneva and M. J. Wainwright (Lossy Compression Data Compression)|Maneva and M. J. Wainwright]] || 2005 || $O(n^{2})$ || $O(n^{2})$ || Exact || Deterministic || [https://ieeexplore.ieee.org/document/1523592 Time] | | [[Maneva and M. J. Wainwright (Lossy Compression Data Compression)|Maneva and M. J. Wainwright]] || 2005 || $O(n^{2})$ || $O(n^{2})$ || Exact || Deterministic || [https://ieeexplore.ieee.org/document/1523592 Time] | ||
|- | |- | ||
| [[ Ciliberti; Mézard (Lossy Compression Data Compression)| Ciliberti; Mézard]] || 2005 || $O(n^{2})$ || | | [[ Ciliberti; Mézard (Lossy Compression Data Compression)| Ciliberti; Mézard]] || 2005 || $O(n^{2})$ || $O(n^{2})$? || Exact || Deterministic || [https://arxiv.org/abs/cond-mat/0504509 Time] | ||
|- | |- | ||
| [[Brute force (Lossy Compression Data Compression)|Brute force]] || 1940 || $O(n*{2}^n)$ || | | [[Brute force (Lossy Compression Data Compression)|Brute force]] || 1940 || $O(n*{2}^n)$ || $O(n*{2}^n)$? || Exact || Deterministic || | ||
|- | |- | ||
| [[Matsunaga; Yamamoto (Lossy Compression Data Compression)|Matsunaga; Yamamoto]] || 2003 || $O(n*{2}^n)$ || exp(n) || Exact || Deterministic || [https://doi.org/10.1109/TIT.2003.815805 Time & Space] | | [[Matsunaga; Yamamoto (Lossy Compression Data Compression)|Matsunaga; Yamamoto]] || 2003 || $O(n*{2}^n)$ || exp(n) || Exact || Deterministic || [https://doi.org/10.1109/TIT.2003.815805 Time & Space] | ||
|- | |- | ||
| [[Sun; M. Shao; J. Chen; K. Wong; and X. Wu (Lossy Compression Data Compression)|Sun; M. Shao; J. Chen; K. Wong; and X. Wu]] || 2010 || $O( | | [[Sun; M. Shao; J. Chen; K. Wong; and X. Wu (Lossy Compression Data Compression)|Sun; M. Shao; J. Chen; K. Wong; and X. Wu]] || 2010 || $O(kmn)$? || $O(kmn)$? || Exact || Deterministic || [https://ieeexplore.ieee.org/document/5474629/ Time] | ||
|- | |- | ||
| [[Miyake 2006 (Lossy Compression Data Compression)|Miyake]] || 2006 || $O(n*{2}^n)$ || | | [[Miyake 2006 (Lossy Compression Data Compression)|Miyake]] || 2006 || $O(n*{2}^n)$ || $O({2}^n)$ || Exact || Deterministic || [https://www.semanticscholar.org/paper/Lossy-Data-Compression-over-Zq-by-LDPC-Code-Miyake/652f0438118898b63126f7261ec4cd2002ff0e0b Time] | ||
|- | |- | ||
| [[Martinian and M. J. Wainwright (Lossy Compression Data Compression)|Martinian and M. J. Wainwright]] || 2006 || $O(n*{2}^n)$ || | | [[Martinian and M. J. Wainwright (Lossy Compression Data Compression)|Martinian and M. J. Wainwright]] || 2006 || $O(n*{2}^n)$ || $O(mn+mk)$? || Exact || Deterministic || [https://arxiv.org/abs/cs/0602046 Time] | ||
|- | |- | ||
| [[Jalali and T. Weissman (Lossy Compression Data Compression)|Jalali and T. Weissman]] || 2008 || $O(n)$ || $O(n)$? || Exact || Deterministic || [https://web.stanford.edu/~tsachy/pdf_files/Lossy%20Source%20Coding%20via%20Markov%20Chain%20Monte%20Carlo.pdf Time] | | [[Jalali and T. Weissman (Lossy Compression Data Compression)|Jalali and T. Weissman]] || 2008 || $O(n)$ || $O(n)$? || Exact || Deterministic || [https://web.stanford.edu/~tsachy/pdf_files/Lossy%20Source%20Coding%20via%20Markov%20Chain%20Monte%20Carlo.pdf Time] | ||
|- | |- | ||
| [[Jalali; A. Montanari; and T. Weissman (Lossy Compression Data Compression)|Jalali; A. Montanari; and T. Weissman]] || 2010 || $O(n)$ || | | [[Jalali; A. Montanari; and T. Weissman (Lossy Compression Data Compression)|Jalali; A. Montanari; and T. Weissman]] || 2010 || $O(n)$ || $O(n)$? || Exact || Deterministic || [https://authors.library.caltech.edu/17983/1/Jalali2010p7459Ieee_T_Inform_Theory.pdf Time] | ||
|- | |- | ||
| [[Korada and R. Urbanke; (Lossy Compression Data Compression)|Korada and R. Urbanke;]] || 2010 || $O(n*{2}^n)$ || $O(N)$ || Exact || Deterministic || [https://arxiv.org/pdf/0903.0307.pdf Time] | | [[Korada and R. Urbanke; (Lossy Compression Data Compression)|Korada and R. Urbanke;]] || 2010 || $O(n*{2}^n)$ || $O(N)$ || Exact || Deterministic || [https://arxiv.org/pdf/0903.0307.pdf Time] | ||
| Line 48: | Line 48: | ||
|} | |} | ||
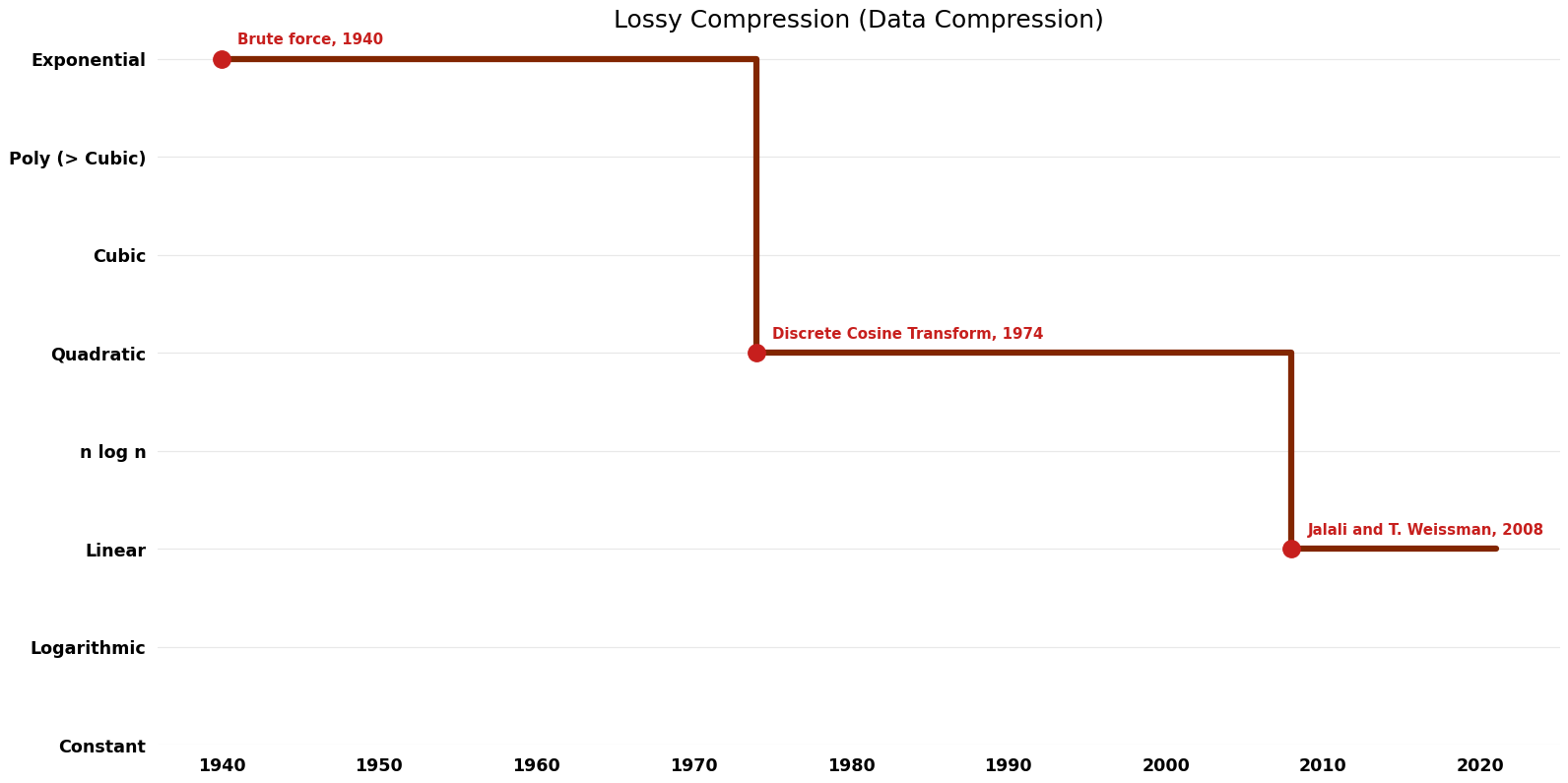
== Time Complexity | == Time Complexity Graph == | ||
[[File:Data Compression - Lossy Compression - Time.png|1000px]] | [[File:Data Compression - Lossy Compression - Time.png|1000px]] | ||
Latest revision as of 10:09, 28 April 2023
Description
The reduction or ideally elimination of redundancies in the original data to result in smaller required storage space is the goal of every compression scheme. There are two categories of data compression: lossy and lossless.
Lossy compression is achieved by only discarding the redundancies and out of human perception information and getting rid of those extra bits.
Related Problems
Related: Lossless Compression
Parameters
$n$: number of items in input series of data
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Gupta; Verdu | 2009 | $O(n^{2} log^{3} n)$ | $O(n)$ | Exact | Deterministic | Time |
| Discrete Cosine Transform | 1974 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | Time |
| Maneva and M. J. Wainwright | 2005 | $O(n^{2})$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Ciliberti; Mézard | 2005 | $O(n^{2})$ | $O(n^{2})$? | Exact | Deterministic | Time |
| Brute force | 1940 | $O(n*{2}^n)$ | $O(n*{2}^n)$? | Exact | Deterministic | |
| Matsunaga; Yamamoto | 2003 | $O(n*{2}^n)$ | exp(n) | Exact | Deterministic | Time & Space |
| Sun; M. Shao; J. Chen; K. Wong; and X. Wu | 2010 | $O(kmn)$? | $O(kmn)$? | Exact | Deterministic | Time |
| Miyake | 2006 | $O(n*{2}^n)$ | $O({2}^n)$ | Exact | Deterministic | Time |
| Martinian and M. J. Wainwright | 2006 | $O(n*{2}^n)$ | $O(mn+mk)$? | Exact | Deterministic | Time |
| Jalali and T. Weissman | 2008 | $O(n)$ | $O(n)$? | Exact | Deterministic | Time |
| Jalali; A. Montanari; and T. Weissman | 2010 | $O(n)$ | $O(n)$? | Exact | Deterministic | Time |
| Korada and R. Urbanke; | 2010 | $O(n*{2}^n)$ | $O(N)$ | Exact | Deterministic | Time |