Non-Comparison Sorting: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Non-Comparison Sorting (Sorting)}} == Description == A sorting algorithm is an algorithm that puts elements of a list in a certain order, not using comparisons between elements (so elements are typically integers or real numbers). == Related Problems == Generalizations: Sorting Related: Comparison Sorting == Parameters == <pre>n: size of list</pre> == Table of Algorithms == {| class="wikitable sortable" style="text-align:center;" width...") |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
== Parameters == | == Parameters == | ||
$n$: size of list | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 28: | Line 28: | ||
| [[Radix Sort (Non-Comparison Sorting Sorting)|Radix Sort]] || 1940 || $O(wn)$ || $O(w+n)$ || Exact || Deterministic || | | [[Radix Sort (Non-Comparison Sorting Sorting)|Radix Sort]] || 1940 || $O(wn)$ || $O(w+n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Naive sorting (Non-Comparison Sorting Sorting)|Naive sorting]] || 1940 || $O( | | [[Naive sorting (Non-Comparison Sorting Sorting)|Naive sorting]] || 1940 || $O(n^{2})$ || $O({1})$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Flash Sort (Non-Comparison Sorting Sorting)|Flash Sort]] || 1998 || $O(n^{2})$ || $O(n)$ || Exact || Deterministic || [http://www.neubert.net/FSOIntro.html Time] | | [[Flash Sort (Non-Comparison Sorting Sorting)|Flash Sort]] || 1998 || $O(n^{2})$ || $O(n)$ || Exact || Deterministic || [http://www.neubert.net/FSOIntro.html Time] & [http://www.neubert.net/FSOIntro.html, Space] | ||
|- | |- | ||
| [[Bead Sort (Non-Comparison Sorting Sorting)|Bead Sort]] || 2002 || $O(n)$ || $O(n^{2})$ || Exact || Deterministic || [https://web.archive.org/web/20170809110409/https://www.cs.auckland.ac.nz/~jaru003/research/publications/journals/beadsort.pdf Time] | | [[Bead Sort (Non-Comparison Sorting Sorting)|Bead Sort]] || 2002 || $O(n)$ || $O(n^{2})$ || Exact || Deterministic || [https://web.archive.org/web/20170809110409/https://www.cs.auckland.ac.nz/~jaru003/research/publications/journals/beadsort.pdf Time] | ||
| Line 36: | Line 36: | ||
| [[Burst Sort (Non-Comparison Sorting Sorting)|Burst Sort]] || 2004 || $O(wn)$ || $O(wn)$ || Exact || Deterministic || [https://dl.acm.org/citation.cfm?doid=1005813.1041517 Time] | | [[Burst Sort (Non-Comparison Sorting Sorting)|Burst Sort]] || 2004 || $O(wn)$ || $O(wn)$ || Exact || Deterministic || [https://dl.acm.org/citation.cfm?doid=1005813.1041517 Time] | ||
|- | |- | ||
| [[Spreadsort (Non-Comparison Sorting Sorting)|Spreadsort]] || 2002 || $O(n | | [[Spreadsort (Non-Comparison Sorting Sorting)|Spreadsort]] || 2002 || $O(n \log n)$ || $O(n)$? || Exact || Deterministic || [https://www.semanticscholar.org/paper/The-Spreadsort-High-performance-General-case-Ross/41f5b49e9843b2d98b6b22a84924dae5761e6e52 Time] | ||
|- | |- | ||
| [[Spaghetti Sort Parallel Implementation (Non-Comparison Sorting Sorting)|Spaghetti Sort Parallel Implementation]] || 1984 || $O(n)$ || $O({1})$ auxiliary? per processor? || Exact || Parallel || [https://link.springer.com/chapter/10.1007/978-94-009-2794-0_11 Time] | | [[Spaghetti Sort Parallel Implementation (Non-Comparison Sorting Sorting)|Spaghetti Sort Parallel Implementation]] || 1984 || $O(n)$ || $O({1})$ auxiliary? per processor? || Exact || Parallel || [https://link.springer.com/chapter/10.1007/978-94-009-2794-0_11 Time] | ||
| Line 42: | Line 42: | ||
|} | |} | ||
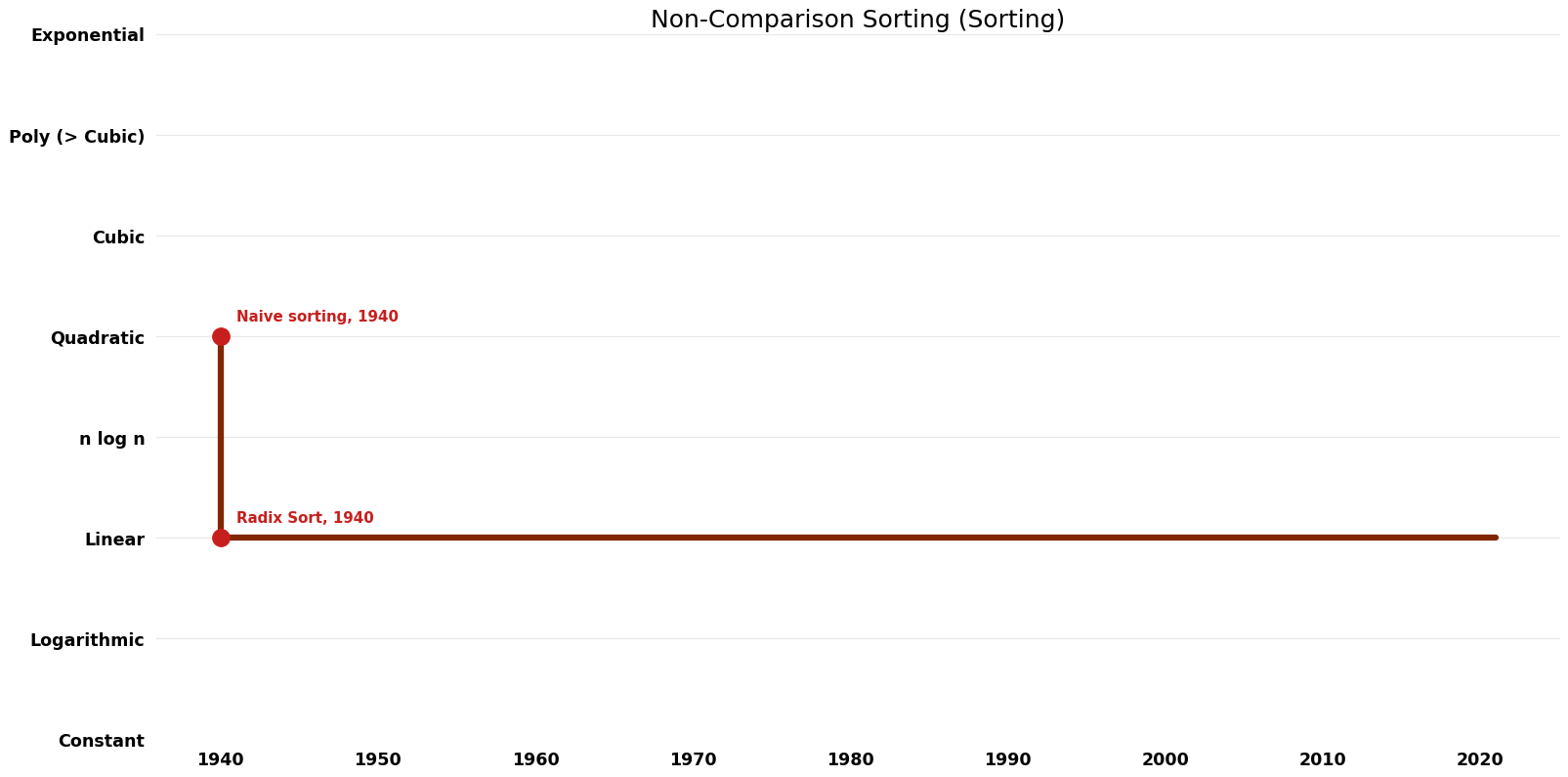
== Time Complexity | == Time Complexity Graph == | ||
[[File:Sorting - Non-Comparison Sorting - Time.png|1000px]] | [[File:Sorting - Non-Comparison Sorting - Time.png|1000px]] | ||
Latest revision as of 10:04, 28 April 2023
Description
A sorting algorithm is an algorithm that puts elements of a list in a certain order, not using comparisons between elements (so elements are typically integers or real numbers).
Related Problems
Generalizations: Sorting
Related: Comparison Sorting
Parameters
$n$: size of list
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Counting Sort | 1954 | $O(n+k)$ | $O(n+k)$ | Exact | Deterministic | Time |
| Bucket Sort | 1940 | $O( n² )$ | $O(n)$ | Exact | Deterministic | |
| Radix Sort | 1940 | $O(wn)$ | $O(w+n)$ | Exact | Deterministic | |
| Naive sorting | 1940 | $O(n^{2})$ | $O({1})$ | Exact | Deterministic | |
| Flash Sort | 1998 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | Time & Space |
| Bead Sort | 2002 | $O(n)$ | $O(n^{2})$ | Exact | Deterministic | Time |
| Burst Sort | 2004 | $O(wn)$ | $O(wn)$ | Exact | Deterministic | Time |
| Spreadsort | 2002 | $O(n \log n)$ | $O(n)$? | Exact | Deterministic | Time |
| Spaghetti Sort Parallel Implementation | 1984 | $O(n)$ | $O({1})$ auxiliary? per processor? | Exact | Parallel | Time |