4-Graph Coloring: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:4-Graph Coloring (Graph Coloring)}} == Description == In this case, we wish to determine whether or not a graph is 4-colorable. == Related Problems == Generalizations: k-Graph Coloring Related: Chromatic Number, 2-Graph Coloring, 3-Graph Coloring, 5-Graph Coloring, #k-Graph Coloring, #2-Graph Coloring, #3-Graph Coloring, #4-Graph Coloring, #5-Graph Coloring == Parameters == <pre>n: number of vertices m: numb...") |
No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
== Parameters == | == Parameters == | ||
$n$: number of vertices | |||
m: number of edges | |||
$m$: number of edges | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 24: | Line 25: | ||
| [[Brute force (4-Graph Coloring Graph Coloring)|Brute force]] || 1852 || $O((m+n)*{4}^n)$ || $O(n)$ auxiliary || Exact || Deterministic || | | [[Brute force (4-Graph Coloring Graph Coloring)|Brute force]] || 1852 || $O((m+n)*{4}^n)$ || $O(n)$ auxiliary || Exact || Deterministic || | ||
|- | |- | ||
| [[Fomin; Gaspers & Saurabh (4-Graph Coloring Graph Coloring)|Fomin; Gaspers & Saurabh]] || 2007 || $O({1.7272}^n)$ || $O(n)$ || Exact || Deterministic || [https://link.springer.com/chapter/10.1007/978-3-540-73545-8_9 Time] | | [[Fomin; Gaspers & Saurabh (4-Graph Coloring Graph Coloring)|Fomin; Gaspers & Saurabh]] || 2007 || $O({1.7272}^n)$ || $O(n)$ || Exact || Deterministic || [https://link.springer.com/chapter/10.1007/978-3-540-73545-8_9 Time] | ||
|- | |- | ||
| [[Lawler (4-Graph Coloring Graph Coloring)|Lawler]] || 1976 || $O((m + n)*{2}^n)$ || $O(n | | [[Lawler (4-Graph Coloring Graph Coloring)|Lawler]] || 1976 || $O((m + n)*{2}^n)$ || $O(n)$ || Exact || Deterministic || [https://www.sciencedirect.com/science/article/pii/002001907690065X?via%3Dihub Time] | ||
|- | |- | ||
| [[Byskov (4-Graph Coloring Graph Coloring)|Byskov]] || 2004 || $O({1.7504}^n)$ || $O(n^{2})$? || Exact || Deterministic || [https://www.sciencedirect.com/science/article/abs/pii/S0167637704000409?via%3Dihub Time] | | [[Byskov (4-Graph Coloring Graph Coloring)|Byskov]] || 2004 || $O({1.7504}^n)$ || $O(n^{2})$? || Exact || Deterministic || [https://www.sciencedirect.com/science/article/abs/pii/S0167637704000409?via%3Dihub Time] | ||
| Line 35: | Line 34: | ||
|} | |} | ||
== Time Complexity | == Time Complexity Graph == | ||
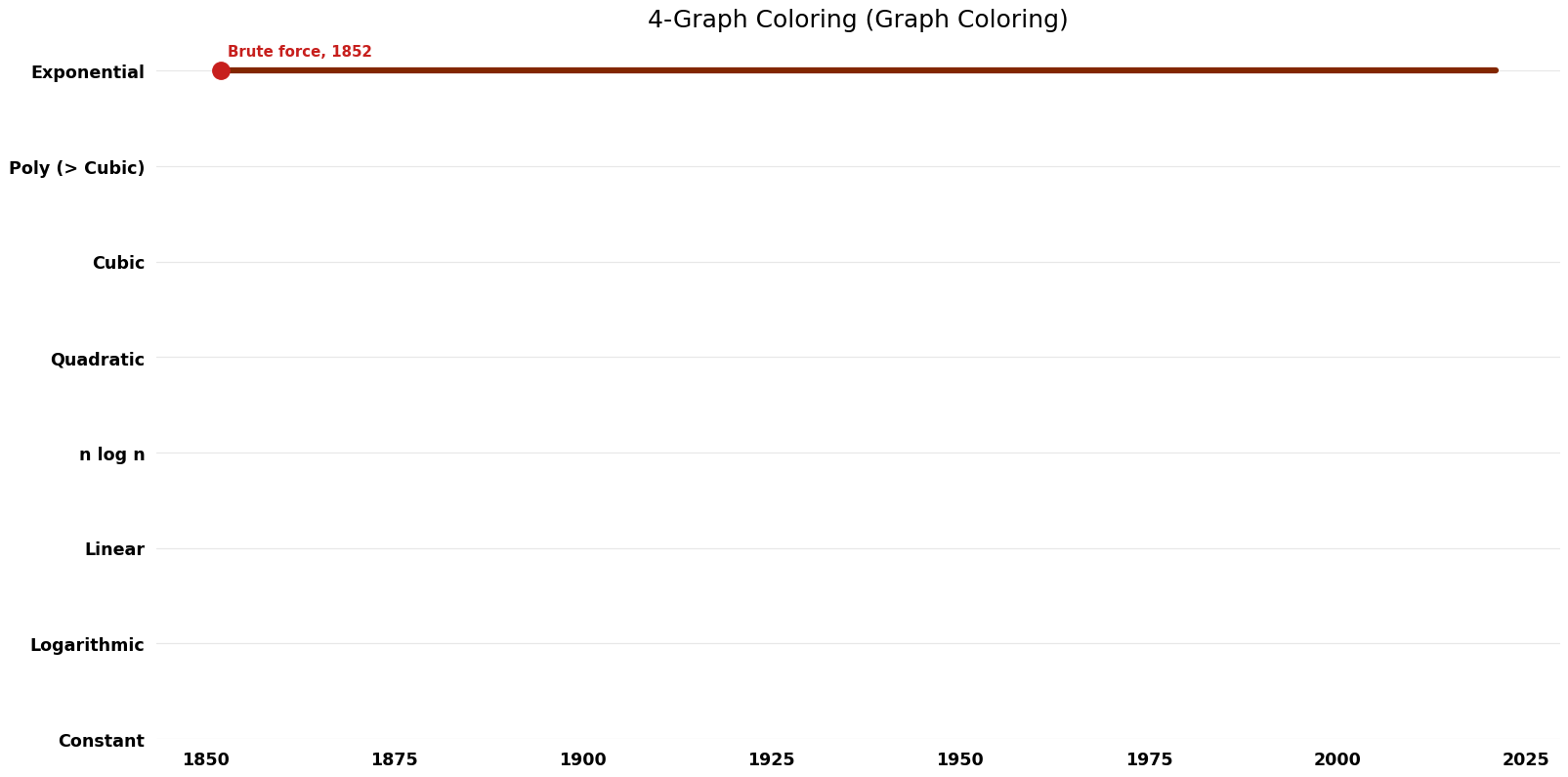
[[File:Graph Coloring - 4-Graph Coloring - Time.png|1000px]] | [[File:Graph Coloring - 4-Graph Coloring - Time.png|1000px]] | ||
== References/Citation == | == References/Citation == | ||
https://link.springer.com/chapter/10.1007/978-3-540-73545-8_9 | https://link.springer.com/chapter/10.1007/978-3-540-73545-8_9 | ||
Latest revision as of 10:12, 28 April 2023
Description
In this case, we wish to determine whether or not a graph is 4-colorable.
Related Problems
Generalizations: k-Graph Coloring
Related: Chromatic Number, 2-Graph Coloring, 3-Graph Coloring, 5-Graph Coloring, #k-Graph Coloring, #2-Graph Coloring, #3-Graph Coloring, #4-Graph Coloring, #5-Graph Coloring
Parameters
$n$: number of vertices
$m$: number of edges
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Brute force | 1852 | $O((m+n)*{4}^n)$ | $O(n)$ auxiliary | Exact | Deterministic | |
| Fomin; Gaspers & Saurabh | 2007 | $O({1.7272}^n)$ | $O(n)$ | Exact | Deterministic | Time |
| Lawler | 1976 | $O((m + n)*{2}^n)$ | $O(n)$ | Exact | Deterministic | Time |
| Byskov | 2004 | $O({1.7504}^n)$ | $O(n^{2})$? | Exact | Deterministic | Time |
Time Complexity Graph
References/Citation
https://link.springer.com/chapter/10.1007/978-3-540-73545-8_9