Greatest Common Divisor: Difference between revisions
Jump to navigation
Jump to search
(Created page with "== Problem Description== The greatest common divisor, sometimes also called the highest common divisor (Hardy and Wright 1979, p. 20), of two positive integers a and b is the largest divisor common to a and b. For example, GCD(3,5)=1, GCD(12,60)=12, and GCD(12,90)=6. The greatest common divisor GCD(a,b,c,...) can also be defined for three or more positive integers as the largest divisor shared by all of them. Two or more positive integers that have greatest common divis...") |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== | {{DISPLAYTITLE:Greatest Common Divisor (Greatest Common Divisor)}} | ||
== Description == | |||
Let $a_1, \ldots, a_m$ be given nonzero integers. Then $g$ is called the greatest common divisor (GCD) of $a_1, \ldots, a_m$ if and only if it is the largest integer that divides all $a_1, \ldots, a_m$. | |||
== | == Parameters == | ||
$n$: sum of number of bits among the integers | |||
== Table of Algorithms == | |||
{| class="wikitable sortable" style="text-align:center;" width="100%" | |||
! Name !! Year !! Time !! Space !! Approximation Factor !! Model !! Reference | |||
|- | |- | ||
| | |||
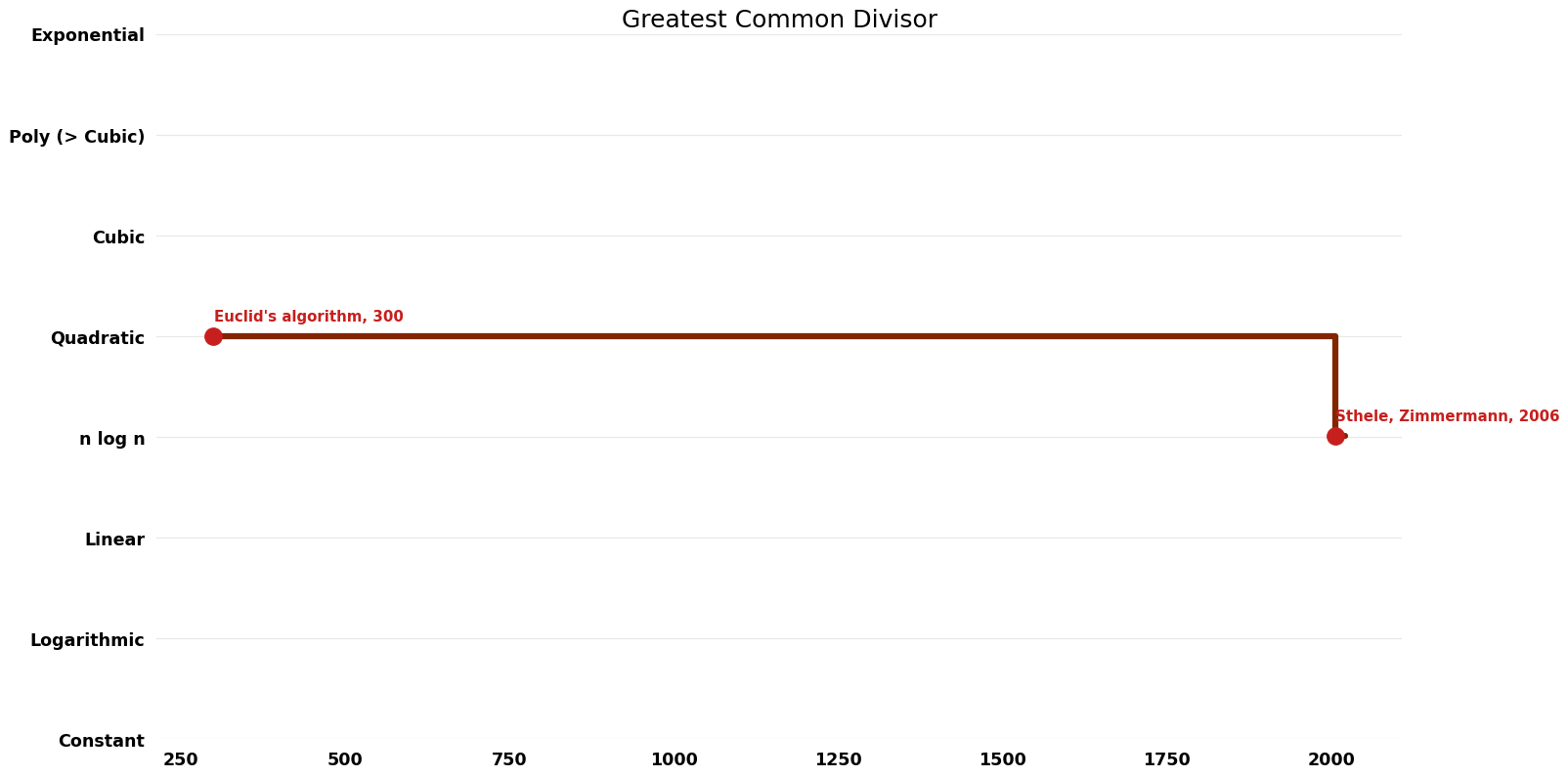
| | | [[Euclid's algorithm (Greatest Common Divisor Greatest Common Divisor)|Euclid's algorithm]] || -300 || $O(n^{2})$ || $O(n)$ || Exact || Deterministic || | ||
| | |||
|- | |- | ||
| | | [[Lehmer's GCD algorithm (Greatest Common Divisor Greatest Common Divisor)|Lehmer's GCD algorithm]] || 1940 || $O(n^{2})$ || $O(n)$ || Exact || Deterministic || | ||
| | |||
| | |||
|- | |- | ||
| | | [[Binary GCD algorithm (Greatest Common Divisor Greatest Common Divisor)|Binary GCD algorithm]] || 1967 || $O(n^{2})$ || $O(n)$ || Exact || Deterministic || [https://arxiv.org/abs/0910.0095 Time] | ||
| | |- | ||
| | | [[Sthele, Zimmermann (Greatest Common Divisor Greatest Common Divisor)|Sthele, Zimmermann]] || 2006 || $O(n \log^{2} n \log \log n)$ || $O(n)$?? || Exact || Deterministic || [https://hal.inria.fr/file/index/docid/71533/filename/RR-5050.pdf Time] | ||
|-|} | |- | ||
|} | |||
== Time Complexity Graph == | |||
[[File:Greatest Common Divisor - Time.png|1000px]] | |||
Latest revision as of 10:12, 28 April 2023
Description
Let $a_1, \ldots, a_m$ be given nonzero integers. Then $g$ is called the greatest common divisor (GCD) of $a_1, \ldots, a_m$ if and only if it is the largest integer that divides all $a_1, \ldots, a_m$.
Parameters
$n$: sum of number of bits among the integers
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Euclid's algorithm | -300 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | |
| Lehmer's GCD algorithm | 1940 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | |
| Binary GCD algorithm | 1967 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | Time |
| Sthele, Zimmermann | 2006 | $O(n \log^{2} n \log \log n)$ | $O(n)$?? | Exact | Deterministic | Time |