Greatest Common Divisor

Description

Let $a_1, \ldots, a_m$ be given nonzero integers. Then $g$ is called the greatest common divisor (GCD) of $a_1, \ldots, a_m$ if and only if it is the largest integer that divides all $a_1, \ldots, a_m$.

Parameters

$n$: sum of number of bits among the integers

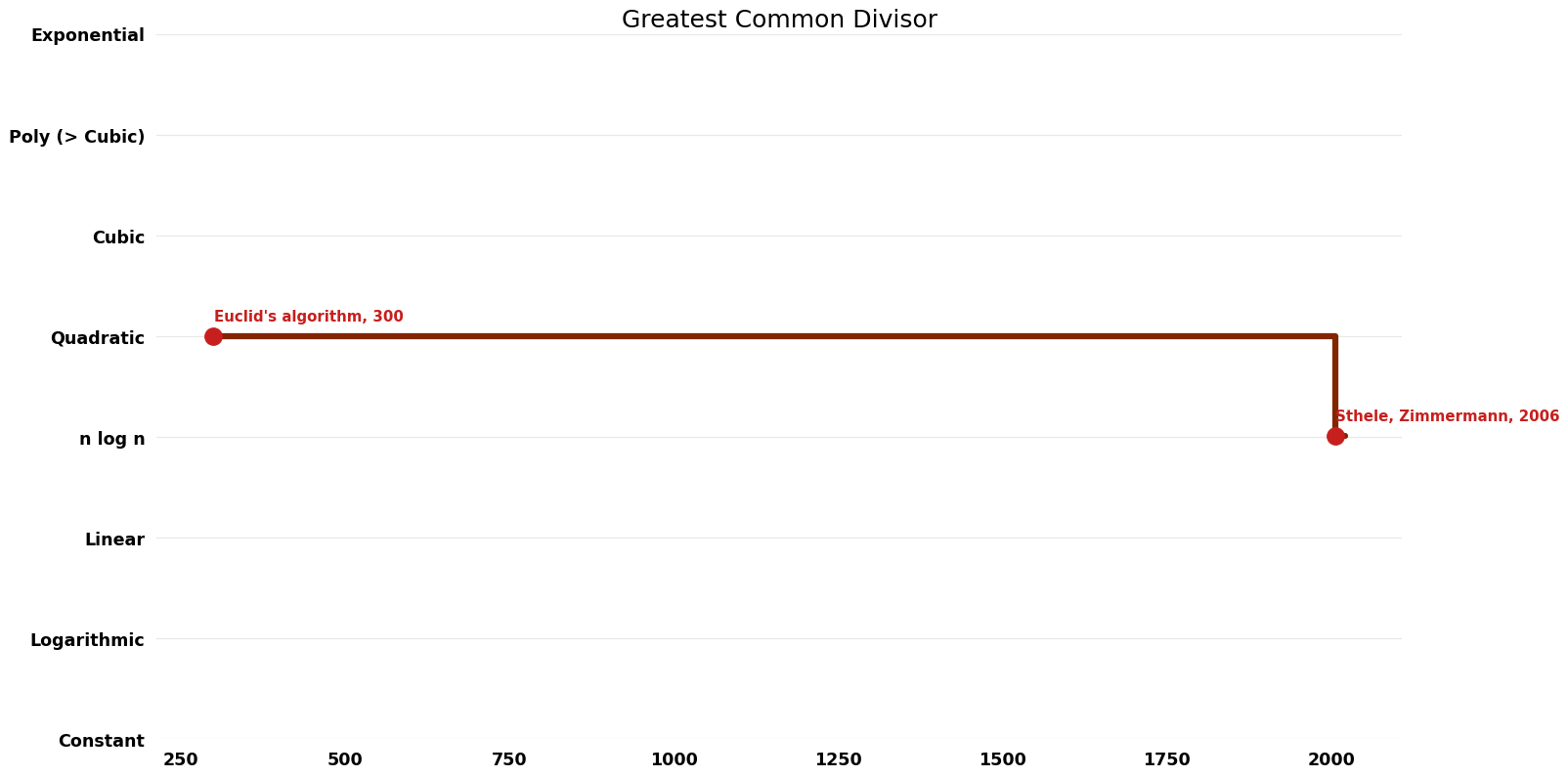
Table of Algorithms

Name	Year	Time	Space	Approximation Factor	Model	Reference
Euclid's algorithm	-300	$O(n^{2})$	$O(n)$	Exact	Deterministic
Lehmer's GCD algorithm	1940	$O(n^{2})$	$O(n)$	Exact	Deterministic
Binary GCD algorithm	1967	$O(n^{2})$	$O(n)$	Exact	Deterministic	Time
Sthele, Zimmermann	2006	$O(n \log^{2} n \log \log n)$	$O(n)$??	Exact	Deterministic	Time

Time Complexity Graph