Change-Making Problem: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:Change-Making Problem (Change-Making Problem)}} == Description == Given an unlimited amount of coins of denominations $c_1, \ldots, c_n$, and a desired sum $S$, find the minimum number of coins necessary to make $S$. == Parameters == <pre>n: number of coin denominations S: sum to be made</pre> == Table of Algorithms == {| class="wikitable sortable" style="text-align:center;" width="100%" ! Name !! Year !! Time !! Space !! Approximation Factor !!...") |
No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
== Parameters == | == Parameters == | ||
$n$: number of coin denominations | |||
S: sum to be made | |||
$S$: sum to be made | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 21: | Line 22: | ||
| [[Dynamic Programming (Change-Making Problem Change-Making Problem)|Dynamic Programming]] || 1953 || $O(Sn)$ || $O(Sn)$ || Exact || Deterministic || [https://dl.acm.org/doi/10.1145/321864.321874 Time] | | [[Dynamic Programming (Change-Making Problem Change-Making Problem)|Dynamic Programming]] || 1953 || $O(Sn)$ || $O(Sn)$ || Exact || Deterministic || [https://dl.acm.org/doi/10.1145/321864.321874 Time] | ||
|- | |- | ||
| [[Probabilistic Convolution Tree (Change-Making Problem Change-Making Problem)|Probabilistic Convolution Tree]] || 2014 || $O(n log n)$ || $O(n log n)$ || || Deterministic || [https://www.ncbi.nlm.nih.gov/pubmed/24626234 Time] & [https://pubmed.ncbi.nlm.nih.gov/24626234/ Space] | | [[Probabilistic Convolution Tree (Change-Making Problem Change-Making Problem)|Probabilistic Convolution Tree]] || 2014 || $O(n \log n)$ || $O(n log n)$ || || Deterministic || [https://www.ncbi.nlm.nih.gov/pubmed/24626234 Time] & [https://pubmed.ncbi.nlm.nih.gov/24626234/ Space] | ||
|- | |- | ||
|} | |} | ||
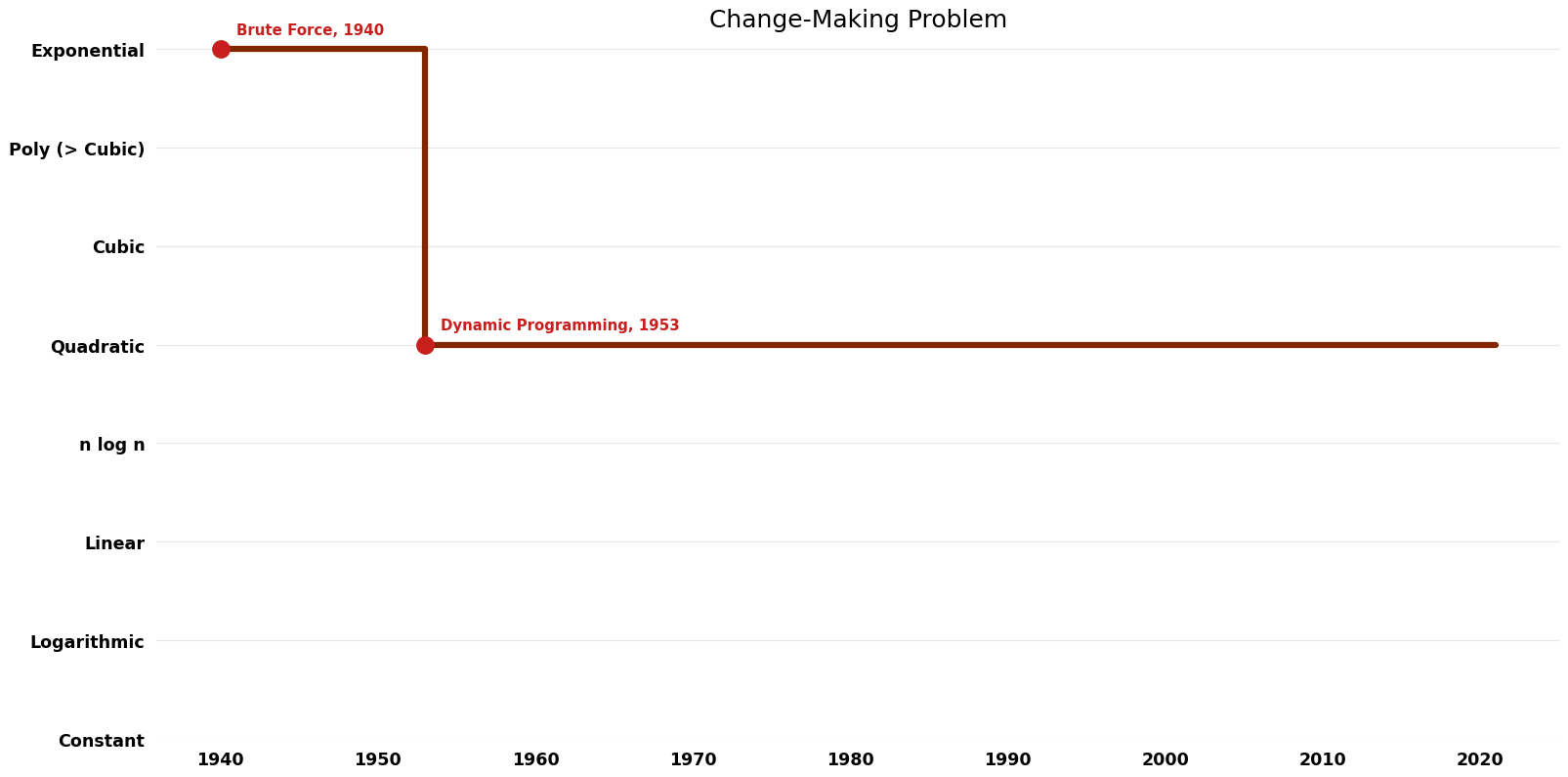
== Time Complexity | == Time Complexity Graph == | ||
[[File:Change-Making Problem - Time.png|1000px]] | [[File:Change-Making Problem - Time.png|1000px]] | ||
Latest revision as of 10:12, 28 April 2023
Description
Given an unlimited amount of coins of denominations $c_1, \ldots, c_n$, and a desired sum $S$, find the minimum number of coins necessary to make $S$.
Parameters
$n$: number of coin denominations
$S$: sum to be made
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Brute Force | 1940 | $O(S^n)$ | $O(n)$ | Exact | Deterministic | |
| Dynamic Programming | 1953 | $O(Sn)$ | $O(Sn)$ | Exact | Deterministic | Time |
| Probabilistic Convolution Tree | 2014 | $O(n \log n)$ | $O(n log n)$ | Deterministic | Time & Space |