1D Maximum Subarray: Difference between revisions
Jump to navigation
Jump to search
(Created page with "{{DISPLAYTITLE:1D Maximum Subarray (Maximum Subarray Problem)}} == Description == Given an array $A$ of length $n$, find $i, j$ with $1\leq i \leq j \leq n$ maximizing $\sum^j_{x=i} A(x)$, that is, find a contiguous subarray of $A$ of maximum sum == Related Problems == Generalizations: Maximum Subarray Related: 2D Maximum Subarray, Maximum Square Subarray == Parameters == <pre>n: length of array</pre> == Table of Algorithms == {| class="wikitable...") |
No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
== Parameters == | == Parameters == | ||
$n$: length of array | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 22: | Line 22: | ||
|- | |- | ||
| [[Brute Force (1D Maximum Subarray Maximum Subarray Problem)|Brute Force]] || 1977 || $O(n^{3})$ || $O({1})$ | | [[Brute Force (1D Maximum Subarray Maximum Subarray Problem)|Brute Force]] || 1977 || $O(n^{3})$ || $O({1})$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Grenander (1D Maximum Subarray Maximum Subarray Problem)|Grenander]] || 1977 || $O(n^{2})$ || $O(n)$ || Exact || Deterministic || | | [[Grenander (1D Maximum Subarray Maximum Subarray Problem)|Grenander]] || 1977 || $O(n^{2})$ || $O(n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Faster Brute Force (via x(L:U) = x(L:U-1)+x(U)) (1D Maximum Subarray Maximum Subarray Problem)|Faster Brute Force (via x(L:U) = x(L:U-1)+x(U))]] || 1977 || $O(n^{2})$ || $O({1})$ | | [[Faster Brute Force (via x(L:U) = x(L:U-1)+x(U)) (1D Maximum Subarray Maximum Subarray Problem)|Faster Brute Force (via x(L:U) = x(L:U-1)+x(U))]] || 1977 || $O(n^{2})$ || $O({1})$ || Exact || Deterministic || [https://dl.acm.org/doi/pdf/10.1145/358234.381162 Time] | ||
|- | |- | ||
| [[Shamos (1D Maximum Subarray Maximum Subarray Problem)|Shamos]] || 1978 || $O( | | [[Shamos (1D Maximum Subarray Maximum Subarray Problem)|Shamos]] || 1978 || $O(n \log n)$ || $O(\log n)$ || Exact || Deterministic || | ||
|- | |- | ||
| [[Kadane's Algorithm (1D Maximum Subarray Maximum Subarray Problem)|Kadane's Algorithm]] || 1982 || $O(n)$ || $O({1})$ auxiliary || Exact || Deterministic || | | [[Kadane's Algorithm (1D Maximum Subarray Maximum Subarray Problem)|Kadane's Algorithm]] || 1982 || $O(n)$ || $O({1})$ auxiliary || Exact || Deterministic || | ||
|- | |- | ||
| [[Perumalla and Deo (1D Maximum Subarray Maximum Subarray Problem)|Perumalla and Deo]] || 1995 || $O(log n)$ || $O(n)$ auxiliary || Exact || Parallel || [https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.24.1291&rep=rep1&type=pdf Time] | | [[Perumalla and Deo (1D Maximum Subarray Maximum Subarray Problem)|Perumalla and Deo]] || 1995 || $O(\log n)$ || $O(n)$ auxiliary || Exact || Parallel || [https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.24.1291&rep=rep1&type=pdf Time] | ||
|- | |- | ||
| [[Gries (1D Maximum Subarray Maximum Subarray Problem)|Gries]] || 1982 || $O(n)$ || $O({1})$ auxiliary || Exact || Deterministic || [https://www.sciencedirect.com/science/article/pii/0167642383900151?via%3Dihub Time] | | [[Gries (1D Maximum Subarray Maximum Subarray Problem)|Gries]] || 1982 || $O(n)$ || $O({1})$ auxiliary || Exact || Deterministic || [https://www.sciencedirect.com/science/article/pii/0167642383900151?via%3Dihub Time] | ||
| Line 38: | Line 38: | ||
| [[Bird (1D Maximum Subarray Maximum Subarray Problem)|Bird]] || 1989 || $O(n)$ || $O({1})$ auxiliary || Exact || Deterministic || [https://dl.acm.org/doi/10.1093/comjnl/32.2.122 Time] | | [[Bird (1D Maximum Subarray Maximum Subarray Problem)|Bird]] || 1989 || $O(n)$ || $O({1})$ auxiliary || Exact || Deterministic || [https://dl.acm.org/doi/10.1093/comjnl/32.2.122 Time] | ||
|- | |- | ||
| [[Ferreira, Camargo, Song (1D Maximum Subarray Maximum Subarray Problem)|Ferreira, Camargo, Song]] || 2014 || $O(log n)$ || $O(n)$ auxiliary || Exact || Parallel || [https://ieeexplore.ieee.org/document/6972008 Time] | | [[Ferreira, Camargo, Song (1D Maximum Subarray Maximum Subarray Problem)|Ferreira, Camargo, Song]] || 2014 || $O(\log n)$ || $O(n)$ auxiliary || Exact || Parallel || [https://ieeexplore.ieee.org/document/6972008 Time] | ||
|- | |- | ||
|} | |} | ||
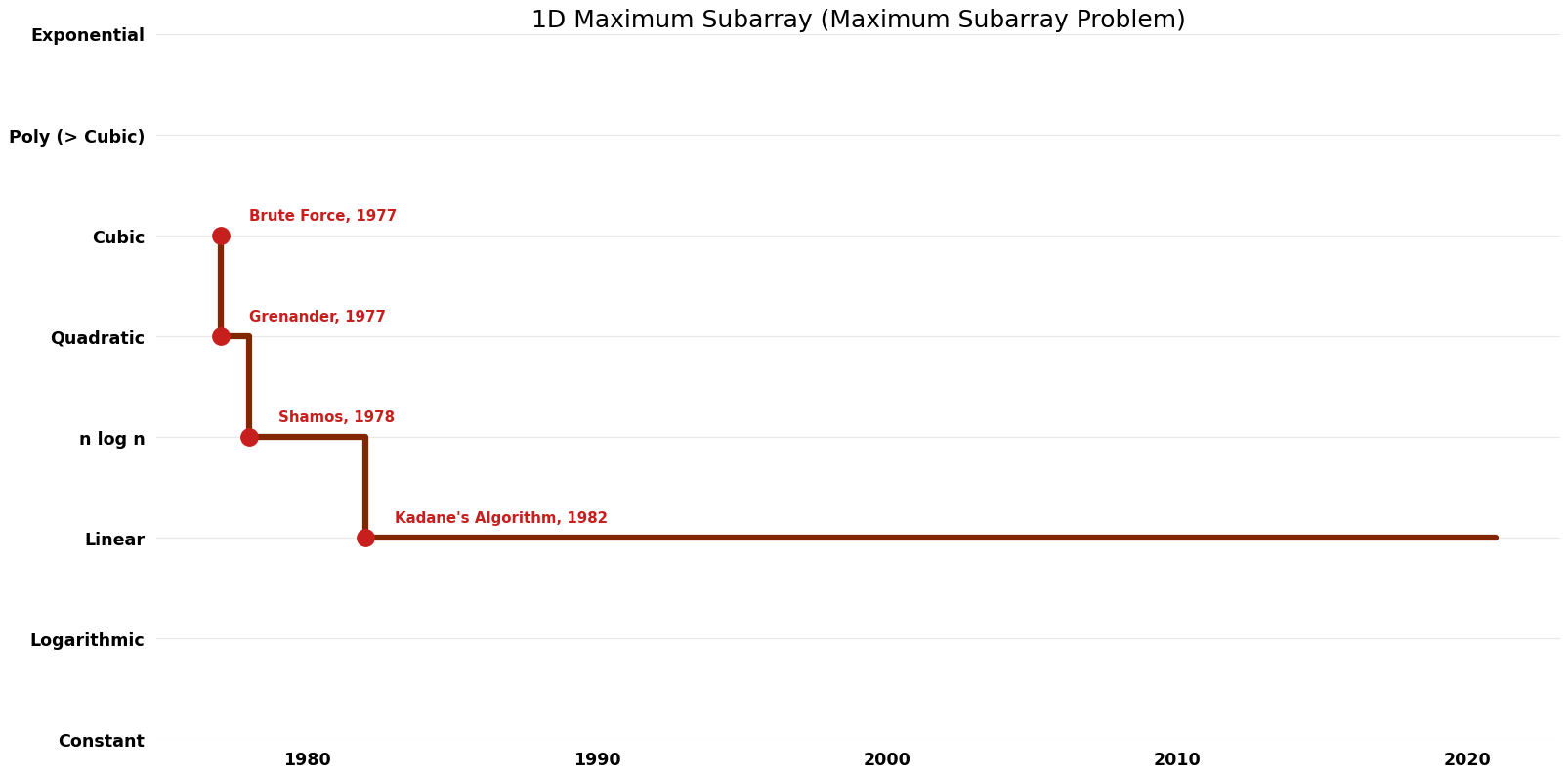
== Time Complexity | == Time Complexity Graph == | ||
[[File:Maximum Subarray Problem - 1D Maximum Subarray - Time.png|1000px]] | [[File:Maximum Subarray Problem - 1D Maximum Subarray - Time.png|1000px]] | ||
Latest revision as of 10:10, 28 April 2023
Description
Given an array $A$ of length $n$, find $i, j$ with $1\leq i \leq j \leq n$ maximizing $\sum^j_{x=i} A(x)$, that is, find a contiguous subarray of $A$ of maximum sum
Related Problems
Generalizations: Maximum Subarray
Related: 2D Maximum Subarray, Maximum Square Subarray
Parameters
$n$: length of array
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Brute Force | 1977 | $O(n^{3})$ | $O({1})$ | Exact | Deterministic | |
| Grenander | 1977 | $O(n^{2})$ | $O(n)$ | Exact | Deterministic | |
| Faster Brute Force (via x(L:U) = x(L:U-1)+x(U)) | 1977 | $O(n^{2})$ | $O({1})$ | Exact | Deterministic | Time |
| Shamos | 1978 | $O(n \log n)$ | $O(\log n)$ | Exact | Deterministic | |
| Kadane's Algorithm | 1982 | $O(n)$ | $O({1})$ auxiliary | Exact | Deterministic | |
| Perumalla and Deo | 1995 | $O(\log n)$ | $O(n)$ auxiliary | Exact | Parallel | Time |
| Gries | 1982 | $O(n)$ | $O({1})$ auxiliary | Exact | Deterministic | Time |
| Bird | 1989 | $O(n)$ | $O({1})$ auxiliary | Exact | Deterministic | Time |
| Ferreira, Camargo, Song | 2014 | $O(\log n)$ | $O(n)$ auxiliary | Exact | Parallel | Time |