CFG Recognition: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 10: | Line 10: | ||
== Parameters == | == Parameters == | ||
n: length of the given string | $n$: length of the given string | ||
$|G|$: size of the grammar | |||
== Table of Algorithms == | == Table of Algorithms == | ||
| Line 29: | Line 31: | ||
[[File:CFG Problems - CFG Recognition - Time.png|1000px]] | [[File:CFG Problems - CFG Recognition - Time.png|1000px]] | ||
== Reductions FROM Problem == | == Reductions FROM Problem == | ||
Latest revision as of 10:09, 28 April 2023
Description
Given a grammar $G$ and a string $s$, determine if the string $s$ can be derived by the grammar $G$.
Related Problems
Related: CFG Parsing
Parameters
$n$: length of the given string
$|G|$: size of the grammar
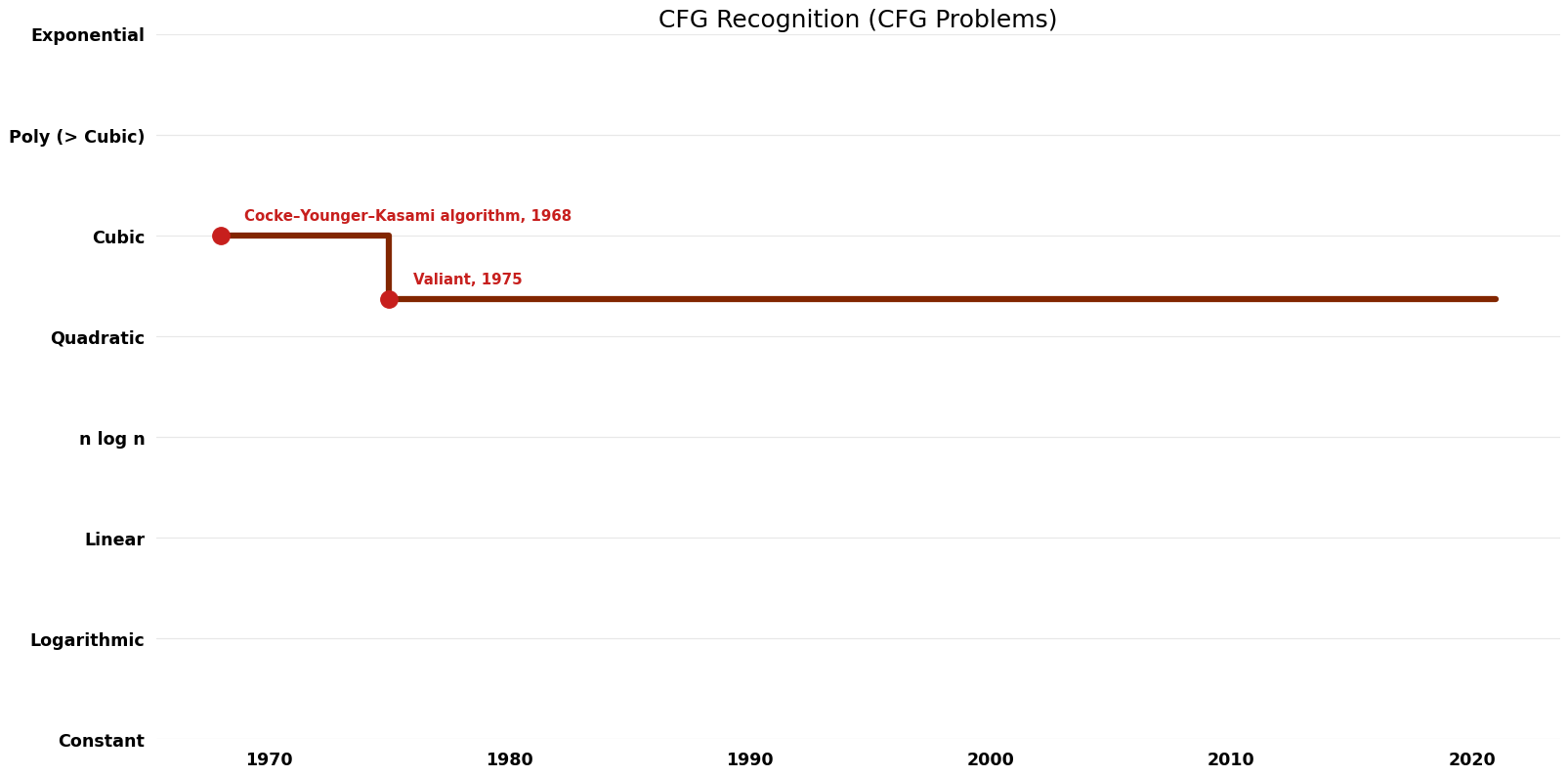
Table of Algorithms
| Name | Year | Time | Space | Approximation Factor | Model | Reference |
|---|---|---|---|---|---|---|
| Cocke–Younger–Kasami algorithm | 1968 | G|)$ | $O(n^{2})$ | Exact | Deterministic | Time & Space |
| Valiant | 1975 | G|)$ where omega is the exponent for matrix multiplication | $O(n^{2})$? | Exact | Deterministic | Time |
Time Complexity Graph
Reductions FROM Problem
| Problem | Implication | Year | Citation | Reduction |
|---|---|---|---|---|
| k-Clique | assume: k-Clique Hypothesis then: there is no $O(N^{\omega-\epsilon}) time algorithm for target for any $\epsilon > {0}$ |
2017 | https://ieeexplore.ieee.org/abstract/document/8104058 | link |
| k-Clique | assume: k-Clique Hypothesis then: there is no $O(N^{\{3}-\epsilon}) time combinatorial algorithm for target for any $\epsilon > {0}$ |
2017 | https://ieeexplore.ieee.org/abstract/document/8104058 | link |
References/Citation
https://linkinghub.elsevier.com/retrieve/pii/S0022000075800468